На этом занятии мы рассмотрим основные понятия и формулы теории вероятности, позволяющие решать текстовые задачи на вероятность. А также рассмотрим методику решения текстовых задач на вероятность. Окружающий нас мир состоит из различных действий и явлений. Например, ежедневно мы можем видеть солнце на небе в ясную погоду или не видеть его в пасмурный день. Действие ежедневного наблюдения солнца на небе называют испытанием. А результат этого действия, солнечно или пасмурно, называют событием. Таким образом, всякое действие, явление или наблюдение с несколькими различными исходами, реализуемое при данных условиях, называется испытанием. Результат этого действия или наблюдения называется событием.

Если событие при заданных условиях может произойти или не произойти, то оно называется случайным. Например, на уроке математики ученик может успешно решить текстовую задачу, а может и не решить, значит, событие "успешно решить текстовую задачу на уроке математики" является случайным. В том случае, когда событие должно непременно произойти, его называют достоверным. Например, событие "в сентябре дети России идут в школу учиться" является достоверным событием, так как выполняется при любых условиях. В том случае, когда событие заведомо не может произойти, его называют невозможным. Например, событие "в полночь над Москвой светит солнце" никогда не может произойти, значит, оно является невозможным событием.

События принято обозначать заглавными буквами латинского алфавита A, B, C, D... Каждое событие имеет числовую характеристику, которую называют вероятностью. Итак, вероятностью события А называется число, которое показывает объективную возможность его свершения. Вероятность обозначают латинской заглавной буквой Р или прописной р и вычисляют по формуле Р от А равно m делённое на n, где m - число благоприятных исходов, n -

Все достоверные события имеют вероятность Р(А) = 1, так как у достоверных событий число благоприятных исходов m и число всевозможных исходов n равны между собой.

Все невозможные события имеют вероятность Р(А) = 0, так как у невозможных событий изменяется в пределах от 0 до 1. События, у которых вероятности всех возможных исходов равны, называются равновозможными. Например, при подбрасывании монеты вероятности выпадения решки или орла равны, значит, исходы выпадения решки или орла будут равновозможными.

События называются несовместными, если каждый раз возможно появление только одного из них. Например, не может быть небо одновременно безоблачным и в дождливых тучах, значит, эти два события несовместны. События называются совместными, если в данных условиях появление одного из этих событий не исключает появление другого при том же испытании. Например, события "яблоко красное" и "яблоко сладкое" могут происходить одновременно, значит, эти события будут совместными.

События называются противоположными, если в условиях испытания они, являясь единственными его исходами, несовместны. Например, при подбрасывании монеты события "выпал орёл" и "выпала решка" являются противоположными. Противоположные события обозначаются одноименной буквой события с чертой над ней. 

Рассмотрим текстовые задачи на вычисление вероятности.

Задача 1.

На 1200 электрических лампочек в среднем приходится 9 бракованных лампочек. Какова вероятность, что наугад взятая лампочка окажется исправной?

Решение:

Пусть событие А - взятая лампочка исправна. Тогда вероятность изъятия исправной лампочки будет именно количество исправных лампочек, равное 1200 минус 9. Получаем m равно 1191. n - количество всех возможных исходов, а значит количество всех лампочек в партии, то есть n равно 1200. Подставив числовые значения переменных в формулу, имеем - вероятность наугад вопрос задачи.

Ответ: 0,9925.

Задача 2.

Юля дважды бросила игральный кубик. В сумме у неё выпало 8 очков. Найти вероятность того, что при первом броске выпало 5 очков.

Решение:

Пусть событие А - при первом броске выпало 5 очков. Для вычисления вероятности вновь 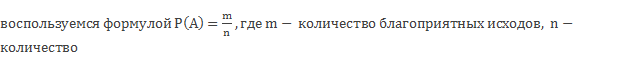всех возможных исходов события А. Чтобы определить числовые значения переменных m и n, рассмотрим все варианты выпадения очков в двух бросках. По условию задачи в результате двух бросков в сумме выпало 8 очков. Так как на гранях игрального кубика возможно выпадение любого числа очков от 1 по 6 включительно, то возможны следующие варианты выпадения очков в двух бросках: 2 и 6, 3 и 5, 4 и 4, 5 и 3, 6 и 2 на кубиках первого и второго бросков соответственно. Тогда получаем, что m равно 5 (количество перечисленных возможных вариантов), а n равно 1 (количество благоприятных из перечисленных - вариант 5 первом броске выпадет 5 очков, равна 0,2. Ответ: 0,2.

Таким образом, на этом занятии мы рассмотрели основные понятия и формулы вычисления вероятности, а также рассмотрели методику решения текстовых задач на вероятность.