На этом занятии мы решим текстовые задачи на равномерное движение по замкнутой дороге, иначе говоря "по окружности".

ЗАДАЧА 1. Кот Базилио и лиса Алиса выехали на велосипедах одновременно в одном направлении из двух диаметрально противоположных точек замкнутой дороги, длина которой равна 5км. Через сколько минут они встретится, если скорость движения Алисы на 6км/ч больше скорости движения кота Базилио?

РЕШЕНИЕ. Решим задачу арифметическим способом. По условию задачи кот Базилио и лиса Алиса выехали на велосипедах одновременно в одном направлении из двух диаметрально противоположных точек замкнутой дороги, длина которой равна 5км. Следовательно, в начале пути их разделяет половина длины трассы, то есть 2,5км. Известно, что скорость движения Алисы на 6км/ч больше скорости движения кота Базилио, значит, каждый час расстояние между ними будет сокращаться на 6 км. Определим, за какое время лиса Алиса сможет преодолеть дистанцию 2,5км и догнать кота Базилио.

Мы ответили на главный вопрос задачи: за 25 минут лиса Алиса догонит кота Базилио.

ЗАДАЧА 2. Маша и медведь решили ежедневно заниматься утренней пробежкой по круговой беговой дорожке. Маша пробегает круг быстрее медведя на 5 минут и через 30 минут после старта впервые обгоняет его. За сколько минут пробегает круг медведь?

РЕШЕНИЕ. Решим задачу алгебраическим способом. Так как по условию задачи надо найти время движения медведя, то логично ввести переменную t– время, за которое преодолевает медведь беговую дорожку, выраженное в минутах. Тогда Маша преодолевает эту дорожку за t– 5 минут, так как она пробегает круг быстрее медведя на 5 минут. В условии задачи нет единиц измерения длины, поэтому удобно длину беговой дорожки принять за 1единицу. Составим таблицу данных задачи.

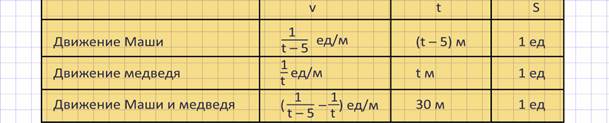
В столбцах будем отмечать v– скорость движения, выраженную в единицах круга в минуту, t– время движения, выраженное в минутах, S– длина пути, выраженная в единицах круга. В строках отметим три вида движения по беговой дорожке: движение Маши, движение медведя и их совместное движение.

В строке движения Маши выразим её скорость.

В строке движения медведя тоже выразим скорость.

Тогда в строке совместного движения скорость их сближения на беговой дорожке равна разности скоростей движения Маши и медведя.

По условию задачи Маша впервые обгоняет медведя через 30 минут после старта, значит, медведь отстаёт от Маши на 1 круг. Следовательно, согласно формулы движения по окружности в одном направлении время между встречами t:

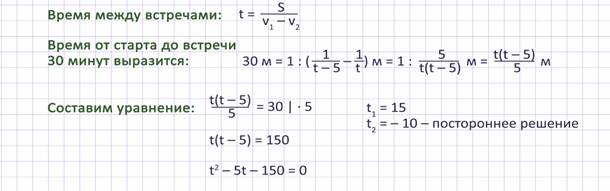
Корень уравнения t = 15 даёт ответ на главный вопрос задачи. Получили, что медведь пробегает беговую дорожку за 15минут. Ответ: 15 минут.

ЗАДАЧА 3. Два бегуна стартуют из одной точки кольцевой дорожки стадиона, а третий бегун стартует одновременно с ними в том же направлении из диаметрально противоположной точки. Пробежав 3 круга, третий бегун впервые после старта догнал второго. Через 2,5 минуты после этого первый бегун впервые догнал третьего. Сколько кругов в минуту пробегает второй бегун, если первый обгоняет его один раз через каждые 6 минут?

РЕШЕНИЕ. Решим задачу алгебраическим способом. В условии задачи не используются единицы измерения длины, поэтому удобно будет длину кольцевой дорожки обозначить за 1 единицу.

Ответом на главный вопрос задачи будет являться значение скорости второго бегуна v2.

По первому условию задачи третий бегун, пробежав 3 круга, впервые после старта догнал второго. Это означает, что за одно и то же время третий бегун пробежал 3 круга, а второй 2,5 круга, так как начало старта второго отличается от начала старта третьего на половину кольцевой дорожки стадиона, то есть на 0,5 единицы. Следовательно, можем составить уравнение:

Так как надо найти v2, то выразим скорость третьего через скорость второго бегуна.

По второму условию задачи через 2,5 минуты после встречи второго и третьего бегунов первый бегун впервые догнал третьего. Это означает, что за одно и то же время третий бегун пробежал 3 плюс 2,5v3 единиц беговой дорожки 3 + 2,5v3, а первый пробежал 3,5 плюс 2,5v3 единиц беговой дорожки 3,5 + 2,5v3, так как положение их стартовых точек отличаются на полкруга, то есть на 0,5. А так как первый догнал третьего бегуна, значит, первый бегун пробежал на 0,5 круга больше. Выразив равное время пробега этих бегунов имеем уравнение

Известно, что в верной пропорции произведение средних членов равно произведению крайних членов. Значит, упрощая произведения, имеем квадратное уравнение 3,6v22 + 4,2v2 – 3 = 0. Разделим каждое слагаемое в обеих частях уравнения на 3 и умножим на5.

Получаем эквивалентное уравнение 6v22 + 7v2 – 5 = 0. Решая данное уравнение имеем корни v2 = и v2 = 0,5. По смыслу задачи скорость должна быть неотрицательной величиной.

Значение второго корня 0,5 является ответом на главный вопрос задачи: 0,5 круга в минуту пробегает второй бегун.

Ответ: 0,5 круга в минуту.

В этом занятии мы решили задачи на движение по замкнутой дороге двух и трёх тел арифметическим и алгебраическим способами.