В этом занятии мы рассмотрим методику решения текстовых задач на оптимизацию с помощью системы неравенств и решим текстовые задачи на оптимизацию различными способами.
Нередко в текстовых задачах на оптимизацию встречаются условия, которые имеют несколько разных ограничений. В таких задачах нельзя обойтись только одним неравенством, а приходится составлять целую систему неравенств:
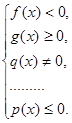
В этой ситуации значительно выручает умение решать систему неравенств.
Решением системы неравенств называется общее решение всех входящих в нее неравенств. Чтобы его найти, надо решить каждое неравенство в отдельности, а затем выбрать те значения, которые удовлетворяют каждому неравенству системы. Для такого отбора общего решения удобно пользоваться геометрическим способом.
Суть этого способа заключается в следующем:

При этом квадратные скобки используются для закрашенных пограничных точек, соответствующих нестрогим знакам не больше ≤ или не меньше ≥, а круглые скобки используются для выколотых пограничных точек, соответствующих строгим знакам больше > или меньше <. Сейчас мы рассмотрим решения текстовой задачи на оптимизацию с помощью системы неравенств.
 Подпишись и будь
в курсе новых событий и новостей!
Подпишись и будь
в курсе новых событий и новостей!