Все текстовые задачи на смеси, сплавы и растворы содержат в себе три основных элемента. Это ЦЕЛОЕ – масса смеси, сплава или раствора, выраженная в граммах, литрах или других мерах веса и объёма; 

ЧАСТЬ– масса определённого вещества в составе смеси, сплава или раствора, выраженная в граммах, литрах или других мерах веса и объёма; 

ДОЛЯ – доля вещества в смеси, сплаве или растворе, выраженная в процентах или, чаще, дробным числом без наименования.

Все три элемента взаимосвязаны между собойформулой

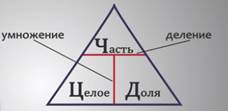
Для более быстрого запоминания этой формулы её удобно записать в треугольник, разбитый на три части. В верхней части запишем ЧАСТЬ, а в двух нижних частях – ЦЕЛОЕ и ДОЛЯ. При этом горизонтальная черта означает деление, а вертикальная – умножение.

Согласно формулы, для того, 

- чтобы найти ЧАСТЬ, надо ЦЕЛОЕ умножить на ДОЛЮ;

- чтобы найти ЦЕЛОЕ, надо ЧАСТЬ разделить на ДОЛЮ;

- чтобы найти ДОЛЮ, надо ЧАСТЬ разделить на ЦЕЛОЕ.

Рассмотрим простейшие задачи на применение этой формулы.

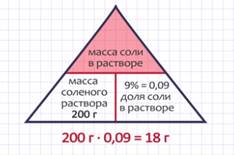
ЗАДАЧА 1. Сколько граммов поваренной соли содержится в 200граммах 9%-ного солёного раствора?

РЕШЕНИЕ.

В этой задаче ЦЕЛОЕ – это масса солёного раствора, 9% = 0,09 – это ДОЛЯ соли в растворе, ЧАСТЬ – это масса соли в растворе. Таким образом, в задаче надо найти часть. Для этого надо ЦЕЛОЕ 200г умножить на ДОЛЮ 0,09. Получили, что 18граммов поваренной соли содержится в 200граммах 9%-ного солёного раствора.

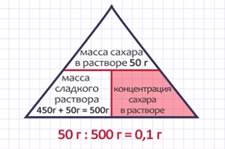
ЗАДАЧА 2. Определить концентрацию раствора 50граммов сахара в 450граммах воды.

РЕШЕНИЕ.

В этой задаче ЦЕЛОЕ – это масса сладкого раствора, равная 450г + 50г =500г, ЧАСТЬ – это масса сахара в растворе 50г. Таким образом, в задаче надо найти ДОЛЮ, которая и является концентрацией сахара в растворе. Для этого надо ЧАСТЬ 50г разделить на ЦЕЛОЕ 500г. Получили, что концентрация раствора равна 0,1 или 10%.

В жизни чаще встречаются более сложные задачи, в которых взаимодействуют несколько смесей, сплавов и растворов. Все такие задачи условно можно разбить на группы: 

-задачи на понижение концентрации;

- задачи на высушивание;

- задачи на смешивание растворов разных концентраций;

- задачи на переливание; 

-задачи на повышение концентрации.

Рассмотрим примеры решения таких задач.

ЗАДАЧА. Сколько килограммов воды надо добавить к 60г 16%-ной соляной кислоты, чтобы получить 10%-ный раствор этой кислоты?

РЕШЕНИЕ.

1 арифметический способ. Так как к соляной кислоте добавляют воду, не содержащую кислоту, то увеличившаяся масса раствора будет обратно пропорциональна концентрации, то есть с увеличением массы раствора концентрация будет уменьшаться во столько же раз. Значит, масса нового раствора относится к массе соляной кислоты 60г так же, как концентрация 16% относится к концентрации 10%. Из пропорции несложно вычислить массу нового раствора из числового выражения произведение 60-ти и 16-ти, делённое на 10. Масса чистой воды равна разности 96-ти и 60-ти, то есть 36г или 0,036кг. 

Мы решили задачу арифметическим способом и ответили на главный вопрос задачи: 0,036кг воды надо добавить в 16%-ную соляную кислоту. 

2 алгебраический способ. Запишем условия задачи в виде таблицы – схемы. Смоделируем данные жидкостей в прямоугольники. В первом прямоугольнике запишем массу соляной кислоты 60г, над ним – концентрацию 16% = 0,16, под ним – массу кислоты в растворе, равную 0,16 умноженной на 60г. Далее поставим знак «плюс», так как по условию к раствору добавляют воду, с отмеченной массой воды mг. В результате должен получиться 10% - ный раствор массой (60 + m)г. Значит, изобразим его в виде прямоугольника с записью 60 + m внутри его, над ним запишем 10% = 0,1, под ним – 0,1(m + 60). Из выражений под прямоугольниками получаем уравнение 0,1 (60 + m) = 0,16∙ 60. Решая его, находим значение переменной m равной 36г.

ЗАДАЧА. Имеется сплав меди с оловом массой 12кг, содержащий 45% меди. Сколько чистого олова надо добавить, чтобы получить сплав, в котором содержится 40% меди?

РЕШЕНИЕ:

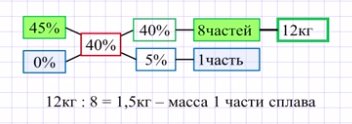
1 схематический способ. Запишем в прямоугольнике концентрацию меди в первом сплаве 45%, ниже в другом прямоугольнике запишем концентрацию меди 0% второго куска, содержащего только олово. В центре второго столбца в прямоугольнике запишем концентрацию нового сплава с концентрацией меди 40%. В третий столбик, применяя правило «крестика», сверху вниз запишем результаты разности 40 – 0% и разности 45 – 40%. Получили числа 40% и 5%. Разделим их на 5 и результаты запишем в 4-й столбик в соответствующих строках. Таким образом, для получения 40% сплава меди с оловом, надо взять 8 частей 45%-ного сплава и 1 часть чистого олова. По условию задачи 45% -й сплав меди с оловом имеет массу 12кг, что составляет 8 частей. Значит, на одну часть приходится 12кг делённое на 8, то есть 1,5кг. Следовательно, чистого олова надо взять 1,5кг. Мы решили задачу схематическим способом.

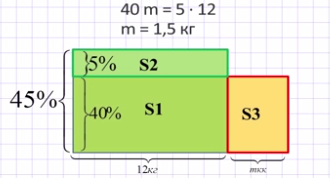
2 геометрический способ. Смоделируем 45%-ный сплав меди с оловом в виде прямоугольника условной длиной в 12кг и условной шириной 45%. На него наложим прямоугольник условной длиной (12 + m)кг и условной шириной 40%. Оба прямоугольника должны быть равновелики, так как содержат одинаковые массы меди. Следовательно, площади их частей S1 = 5∙12 и S2= 40m равны между собой. Значит, решая уравнение 40m = 5∙12, имеем, что m = 1,5. Таким образом, с помощью геометрического способа мы ответили на главный вопрос задачи 1,5 кг чистого олова надо добавить для получения 40% -ного содержания меди в сплаве.

ЗАДАЧА. Индийский чай дороже грузинского на 25%. В каких пропорциях нужно смешать индийский чай с грузинским, чтобы получить чай, который дороже грузинского на 20%.

РЕШЕНИЕ:

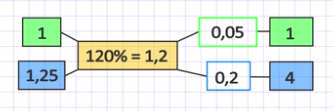
Цена индийского чая дороже на 25%, значит, составляет 125% от цены грузинского чая, следовательно, доля цены индийского чая равна 1,25, а доля цены грузинского чая равна 1-ой единице. Решим задачу схематическим способом по правилу «крестика». В первом столбике друг под другом запишем доли цен грузинского и индийского чая соответственно, то есть 1 и 1,25. Во втором столбике в центре поместим долю смеси, которая дороже грузинского чая на 20%, то есть 120% равно 1,2. В третьем столбике «крестиком» друг под другом запишем разности 1,25 – 1,2 = 0,05 и 1,2 – 1 = 0,2. Чтобы избавиться от дробных чисел, домножим оба результата третьего столбика на 20. Получили числа 1 и 4, которые показывают доли грузинского и индийского чая соответственно для получения нужной смеси. Таким образом, мы ответили на главный вопрос задачи индийский и грузинский чай надо взять в отношении 4 к 1 соответственно.

Подведём итоги. На этом занятии мы познакомились с элементами текстовых задач на смеси, сплавы и растворы, а также с формулой, связывающей эти элементы. Познакомились с методикой решения текстовых задач на смеси, сплавы и растворы различными способами.