В этом занятии мы рассмотрим текстовые задачи на применение формул арифметической прогрессии. Для начала вспомним, что такое арифметическая прогрессия, а затем рассмотрим формулы, связанные с ней. Множество чисел, каждое из которых имеет номер, называется числовой последовательностью.

Например, в последовательности чисел –2; 17; 22; 19 член последовательности –2 имеет номер 1, так как стоит на первом месте, член последовательности 22 имеет номер 3 так как стоит на 3-ем месте.

Обозначают члены последовательности прописными латинскими буквами с нижним индексом порядкового номера. Например, член последовательности х7 стоит на седьмом месте последовательности (хn). Из всех последовательностей выделяют две особые: арифметическую прогрессию и геометрическую прогрессию.

Арифметической прогрессией (an) а1 а2 ...аn-1anan+1 ...называется последовательность чисел, в которой каждый член, начиная со второго, отличается от предыдущего на одно и то же число.

Это число называется разностью арифметической прогрессии и обозначается латинской буквой d.

Например, в арифметической прогрессии

первый член равен 5, разность арифметической прогрессии равна разности последующего члена прогрессии и предыдущего то есть

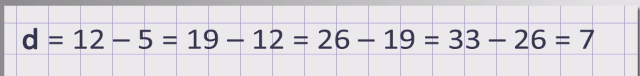
Зная первый член a1, разность d и номер n члена арифметической прогрессии можно вычислить член прогрессии an, стоящий на n - м месте, по формуле аn= a1 + (n– 1)d. Сумма n членов арифметической прогрессии Sn вычисляется как произведение полусуммы первого и последнего членов прогрессии на количество членов прогрессии

Или

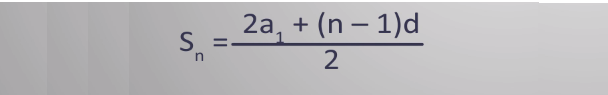
В решении задач на арифметическую прогрессию полезно помнить основное свойство членов прогрессии, что каждый член прогрессии, начиная со второго, равен среднему арифметическому рядом стоящих членов, то есть их полусумме

Рассмотрим примеры текстовых задач на использование формул арифметической прогрессии.

ЗАДАЧА 1. Бригада маляров красит забор длиной 450 метров, ежедневно увеличивая норму покраски на одно и то же число метров. Известно, что за первый и последний день в сумме бригада покрасила 50 метров забора. Определите, сколько дней бригада маляров красила весь забор.

РЕШЕНИЕ. По условию задачи бригада маляров красит забор, ежедневно увеличивая норму покраски на одно и то же число метров. Значит, если последовательно друг за другом выписать ежедневное количество метров выкрашенного забора, начиная с первого дня, то мы получим последовательность чисел, которая является арифметической прогрессией. Так как весь объём работы составляет 450 м забора, то длина забора смоделируется в сумму n конечных членов этой прогрессии, где число

n моделирует количество дней работы маляров и является главным вопросом задачи. Воспользуемся формулой суммы n первых членов арифметической прогрессии, Sn

Мы ответили на главный вопрос задачи: бригада маляров красила забор 18 дней.

ЗАДАЧА 2. На подготовку к олимпиаде по математике школьнику понадобилось 12 недель, за это время он прорешал 840 задач. Приобретая опыт, в каждую последующую неделю, начиная со второй, он решал на 10 задач больше, чем в предыдущую. Какое количество задач в этом темпе прорешал школьник за оставщиеся до олимпиады 3 недели?

РЕШЕНИЕ. Смоделируем задачу, переведем на язык математики. По условию школьник в каждую последующую неделю, начиная со второй, решал на 10 задач больше, чем в предыдущую. Значит, последовательность еженедельного количества прорешанных задач моделируется в арифметическую прогрессию с разностью d, равной 10-ти. Еще по условию задачи известно, что школьник за 12 недель прорешал 840 задач, значит, количество членов прогрессии n равно 12, а сумма двенадцати членов прогрессии равна 840. Значит, из формулы суммы членов прогрессии Sn

То есть получили, что в первую неделю школьник решил 15 задач.

Количество задач за оставщиеся до олимпиады 3 недели составляют другую арифметическую прогрессию (хn) из трёх членов, у которой первый член равен по значению количеству задач, решённых в 10-ю неделю, то есть x1 = а10. Последним третьим членом этой новой прогрессии является количество задач, решённых школьником в двенадцатую неделю, то есть x3 = а12.

Вычислим значения 10-го и 12-го членов прогрессии по формуле n-го члена

аn= a1 + (n– 1)d.

Имеем, что

а10 = 15 + 9·10 = 105

а12 = 15 + 11·10 = 125.

Тогда сумма последних 3-х членов прогрессии равна

Мы ответили на главный вопрос задачи за оставшиеся до олимпиады 3 недели школьник прорешал 345 задач. Ответ: 345 задач.

ЗАДАЧА 3. В течение календарного года налоги, подлежащие уплате фирмой "Папа Карло", увеличиваются ежемесячно на одну и ту же величину. Владелец этой фирмы Буратино заплатил за апрель 5500 рублей, а в июле и августе в сумме 13400 рублей. Какую сумму налогов должен заплатить Буратино в ноябре?

РЕШЕНИЕ. По условию задачи в течение календарного года налоги, подлежащие уплате фирмой "Папа Карло", увеличиваются ежемесячно на одну и ту же величину. Значит, суммы ежемесячных выплат налогов фирмой составляют арифметическую прогрессию, в которой первый член равен сумме выплат в январе, второй - в феврале и так далее. Известно, что владелец этой фирмы Буратино заплатил за апрель 5500 рублей, следовательно, четвёртый член прогрессии равен 5500. Воспользуемся формулой n-го члена арифметической прогрессии аn= a1 + (n – 1)d. Имеем, а4 = a1 + 3d = 5500.

Так как известно, что в июле и августе Буратино выплатил налог в сумме 13400 рублей, выразим через первый член и разность арифметической прогрессии сумму 7-го и 8-го членов.

Согласно формулы n-го члена арифметической прогрессии имеем,

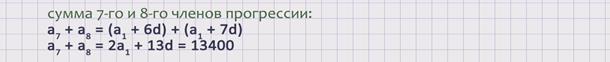
Главным вопросом задачи является сумма налогов, которую должен заплатить Буратино в ноябре.

Но можно найти искомую величину более рациональным способом.

Заметим, что левые части обоих уравнений отличаются друг от друга на a1 + 10d, а это выражение и является искомым. Значит, можно из обеих частей второго уравнения вычесть соответствующие части первого уравнения.

Тогда имеем, a1 + 10d= 13400 – 5500 = 7900. Мы ответили на главный вопрос задачи: в ноябре Буратино выплатит налог в размере 7900 рублей.

Ответ: 7900 рублей.

На этом занятии мы решили несколько текстовых задач на применение формул арифметической прогрессии.