ЗАДАЧА 1. Три поросёнка Ниф-Ниф, Наф-Наф и Нуф-Нуф решили своими руками сделать игрушки для новогодней ёлки. Ниф-Ниф изготовлял 5 игрушек в час, а Наф-Наф 8 игрушек в час. Ниф-Ниф и Наф-Наф начали работу одновременно, а Нуф-Нуф –на полчаса позже. Через некоторое время Нуф-Нуф догнал по количеству изготовленных игрушек Ниф-Нифа, а ещё через полтора часа после этого догнал и Наф-Нафа. Определите производительность труда Нуф-Нуфа.
Р Е Ш Е Н И Е :
Решим задачу алгебраическим способом.
Введём переменные:
р – производительность труда Нуф-Нуфа игрушек в час.
t – время в часах, через которое Нуф-Нуф догнал по количеству изготовленных игрушек Ниф-Нифа.
По условию задачи Нуф-Нуф начал работать на полчаса позже, значит, он проработал до этого момента (t –0,5) часов. Так как Нуф-Нуф догнал по количеству изготовленных игрушек Ниф-Нифа, значит, можно составить уравнение:
p(t – 0,5) = 5t.
По условию задачи через полтора часа Нуф-Нуф догнал по количеству игрушек и Наф-Нафа. Значит, за время работы Нуф-Нуф сделал p(t +1) игрушек, а Наф-Наф 8(t + 1,5) игрушек. Мы получили второе уравнение:
p(t +1) = 8(t + 1,5).
По условию задачи надо найти значение переменной р. Следовательно, из каждого полученного уравнения выразим переменную t через переменную р. Из первого уравнения имеем:
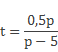
Из второго уравнения получим
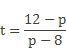
Левые части выражений равны, следовательно, и правые части тоже равны. Мы получили пропорциональное уравнение с одной переменной р, а именно:
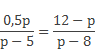
Известно, что в верной пропорции произведение крайних членов равно произведению средних членов. Значит, получим уравнение:
0,5р(р – 8) = (12 – р)(р – 5).
Раскрыв скобки, перенесём всё в левую часть уравнения и приведём подобные члены. Получаем квадратное уравнение
1,5р2 – 21р + 60 = 0.
Обе части уравнения умножим на две третьих. Имеем квадратное уравнение:
р2 –14р + 40 = 0; с корнями р1 = 4 и р2 = 10.
По условию задачи Нуф-Нуф начал работать позже и догнал по количеству изготовленных игрушек своих друзей, следовательно, его производительность должна быть больше производительности и Ниф-Нифа, и Наф-Нафа. Значит, по смыслу задачи значение р должно быть больше 8-ми. Получили, что р = 4 является посторонним решением, а значение р = 10даёт ответ на главный вопрос задачи: производительность труда Нуф-Нуфа 10 игрушек в час.
О Т В Е Т : 10 игрушек в час.
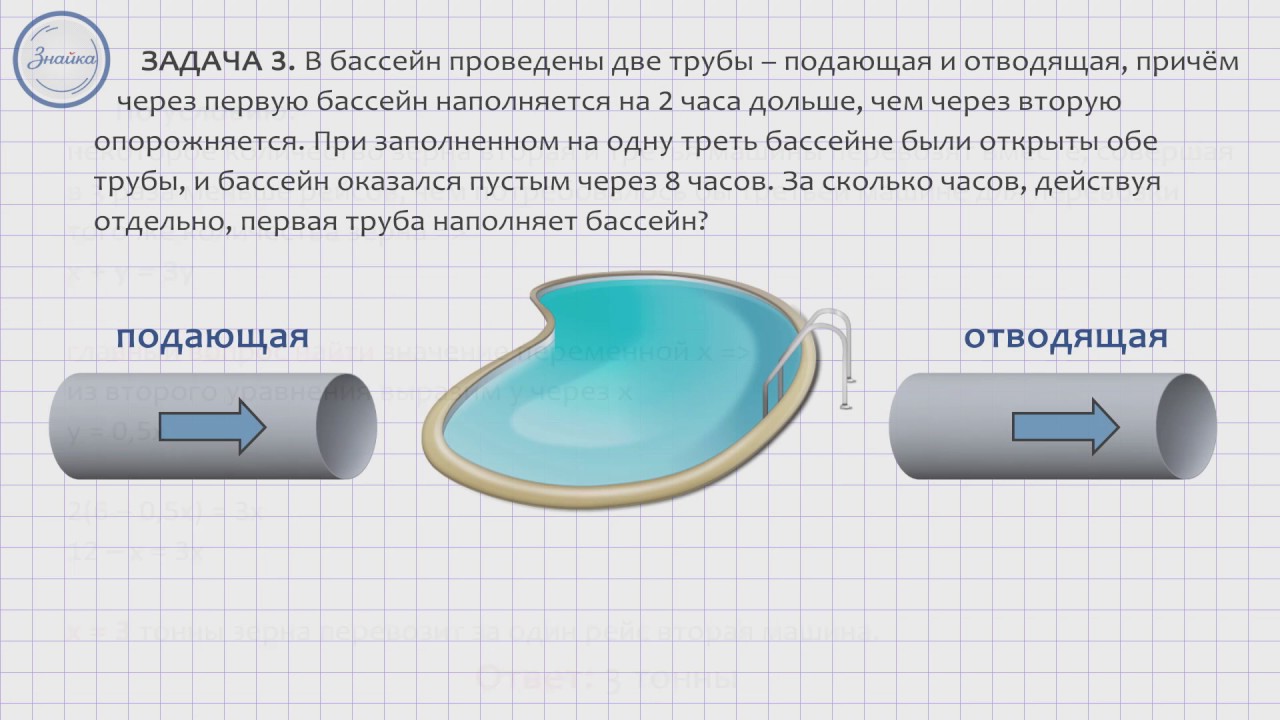
ЗАДАЧА 2. . В бассейн проведены две труб – подающая и отводящая, причём через первую бассейн наполняется на 2 часа дольше, чем через вторую опорожняется. При заполненном на одну треть бассейне были открыты обе трубы, и бассейн оказался пустым через 8 часов. За сколько часов, действуя отдельно, первая труба наполняет бассейн?
Р Е Ш Е Н И Е :
Решим задачу алгебраическим способом.
Введём переменные.
Главный вопрос задачи заключается в определении количества часов, за которое первая труба, действуя отдельно, наполняет бассейн. Значит:
t – время работы первой трубы для заполнения бассейна в часах;
t – 2 – время слива воды из бассейна через вторую трубу в часах, так как по условию задачи через первую бассейн наполняется на 2 часа дольше, чем через вторую опорожняется.
В условии задачи отсутствуют единицы измерения объёма бассейна, значит, весь объём бассейна примем за 1 единицу. При заполненном на одну треть бассейне были открыты обе трубы, и бассейн оказался пустым через 8 часов. Следовательно, 2/3 бассейна заполняется
![]()
Выразим объём бассейна через производительность подающей трубы, а именно, как одна третья бассейна плюс её производительность 1 делённая на t и умноженная на время работы трубы 8 часов
![]()
Объём бассейна через производительность отводящей трубы выразится как её производительность 1 деленная на (t – 2) и умноженная на время работы 8 часов
![]()
![]()
![]()
Приведём дроби к общему знаменателю и упростим числитель.
Тогда получим уравнение
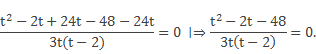
Известно, что дробь равна 0, если числитель равен 0. Решая квадратное уравнение
t2 – 2t – 48 = 0,
получаем корни t1 = – 6 и t2 = 8. По смыслу задачи значение времени t должно быть неотрицательной величиной, значит, корень t = – 6 является посторонним решением. А корень t = 8даёт ответ на главный вопрос задачи: первая труба заполняет бассейн за 8 часов.
О Т В Е Т : 8 часов.
ЗАДАЧА 3. Одновременно зажжены две свечи одинаковой длины, но разной толщины. Одна сгорает за 5 часов, а другая – за 4 часа. Через сколько минут были погашены одновременно две свечи, если от первой свечи остался огарок в 4 раза длиннее, чем от второй?
Р Е Ш Е Н И Е :
Решим задачу алгебраическим способом.
Введём переменную. Так как главным вопросом является количество минут одновременного горения свечек, то логично за переменную t часов обозначить это время.
t – количество минут одновременного горения свечек в часах.
По условию задачи две свечи одинаковой длины, причём их длина не выражена в единицах измерения, значит, примем длину свечей за 1 единицу. Также в условии сказано, что свечи разной толщины и одна из них сгорает за 5 часов, а другая – за 4 часа. Следовательно,
![]()
![]()
Выразим длину огарков после горения свечей в течение t часов.
![]()
![]()
По условию задачи от первой свечи остался огарок в 4 раза длиннее, чем от второй. Значит, составим уравнение
![]()
Раскрыв скобки и проведя алгебраические преобразования, получаем корень уравнения
![]()
Мы ответили на главный вопрос задачи: через 3,75 часа огарок первой свечи будет в 4 раза длиннее огарка второй свечи. Выразим результат времени в минутах, для этого 3,75 умножим на 60 минут. Получаем 225 минут.
О Т В Е Т : 225 минут.
 Подпишись и будь
в курсе новых событий и новостей!
Подпишись и будь
в курсе новых событий и новостей!