Пересечением множествА и В называется множество, состоящее из всех общих элементов множества А и В, то есть из всех элементов, которые принадлежат и множеству А, и множеству В. A∩B = {x ∣ x∊A и x∊B}.

Пересечение множеств обозначают двухпалой вилкой, направленной вниз ∩.

ПРИМЕР 1.

Найти пересечение множеств А и В, если

а) А - множество различных букв, используемых в слове "ЗНАЙКА", В - множество различных букв, используемых в слове "ОБУЧАЙКА"; 

б) А - множество всех двузначных чисел, В - множество чисел, кратных 11; 

в) А = [пи; корень квадратный из 41], В = N .

РЕШЕНИЕ.

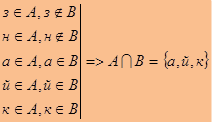
а) Выпишем множество различных букв в слове "ЗНАЙКА". Получаем, что множество А состоит из букв з, н, а, й, к. A=. Выпишем множество различных букв в слове "ОБУЧАЙКА". Получаем, что множество состоит из букв о, б, у, ч, а, й, к. B=. Рассмотрим поочерёдно каждый элемент множества А и выясним, входят ли они во множество В. Буква "з" принадлежит множеству А, но не принадлежит множеству В, значит, не является общим элементом для этих двух множеств. Буква "а" принадлежит и множеству А, и множеству В, значит, является общим элементом для множества А и множества В. Аналогично рассуждая, проверяем каждую букву множеств А и В. Получаем, что буквы а, й, к являются общими для множества А и множества В, значит, множество из этих букв является пересечением двух множеств А и В.

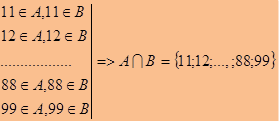
б) Распишем множество двузначных чисел А как 10, 11, 12, 13, . . . 96, 97, 98, 99 и множество чисел, которые делятся на 11 - множество В как 11, 22, 33, . . . 88, 99, 110, . . . Перебираем каждый элемент множества А, потому что оно содержит меньше элементов, чем множество В, получаем, что числа 11, 12, ..., 88, 99 являются элементами и множества А и множества В. Значит, эти общие элементы составляют множество являющееся пересечением двух данных множеств А и В.

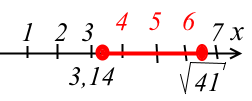
в) На числовой прямой отметим отрезок от пи до корня квадратного из 41. Число пи принадлежит множеству А, но не является натуральным числом, значит, не принадлежит множеству В. Корень квадратный из 41 также принадлежит множеству А и расположен между натуральными числами 6 и 7, значит, он не является элементом множества В. Тогда во множество А войдут натуральные числа 4, 5, 6.

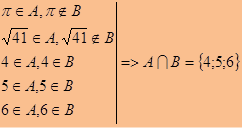
Эти три числа и составляют множество являющееся пересечением двух множеств А и В.