
На этом занятии мы научимся строить графики модульной линейной функции, познакомимся с алгоритмом решения линейного модульного неравенства с помощью графиков и разберём примеры решения модульных линейных неравенств графическим способом.
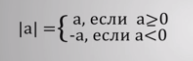
Вспомним аналитическое определение модуля: модулем числа а называется само число а, если оно неотрицательное и противоположное числу а, если оно отрицательное.
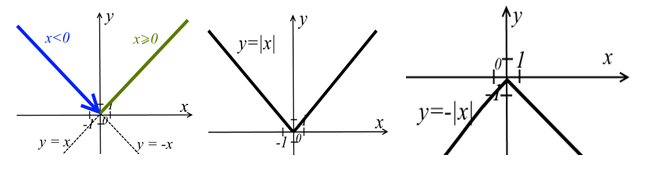
Следовательно, модульная функция у = |x| будет кусочно-линейной функцией, так как её составляющими являются две линейные функции у = х и у = –х, определённые на х ≥ 0 и х < 0 соответственно. Графиком этой функции являются два луча, образующие угол с вершиной в начале координат, проходящие через точки (–1; 1) и (1; 1).
Рассмотрим линейное модульное неравенство|x– р| > q.
В этом неравенстве может стоять не только знак больше, но и знак меньше, не больше или не меньше.
Решим это неравенство графически. Для этого надо:
1. В одной системе координат построить графики функций у = |x – p| и у = q. Графиком у = |x– p| является угол с вершиной в точке (р; 0) и сторонами у = х – р и у = –х + р, направленными вверх, так как перед модулем нет знака, а значит подразумевается знак "+". Если перед модулем стоит знак "–", то стороны угла должны быть направлены вниз.
2. Выделить ту часть графика, которая соответствует знаку неравенства: в неравенстве
|x– p| > q знак больше надо понимать, что точки графика модульной функции у = |x– p| должны быть выше графика у = q. В этом случае и во всех строгих неравенствах точка пересечения графиков не входит в область решения. Нестрогие знаки неравенства предполагают включение точки пересечения графиков в область решения модульного неравенства.
3.Решением исходного модульного неравенства являются все абсциссы точек, то есть значения х, выделенной области графика.
 Подпишись и будь
в курсе новых событий и новостей!
Подпишись и будь
в курсе новых событий и новостей!