Модульным рациональным неравенствомназывается неравенство вида |f(x)| < a, где f(x)- многочлен.

Модульным дробно-рациональным неравенствомназывается неравенство вида ∣р(х)/q(х)∣ < a, где p(x) и q(x)- многочлены.

В этих неравенствах может стоять не только знак меньше, но и знак больше, не больше или не меньше.

Для решения этих неравенств с помощью графиков надо:

1. В одной системе координат построить графики модульной функции у =∣f(x)∣ или 

у = ∣р(х)/q(х)∣ и линейной функции у = а. Чтобы построить график первой функции, надо построить график подмодульной функции и отобразить часть этого графика, расположенного ниже оси абсцисс Ох в верхнюю полуплоскость относительно оси Ох. Полученная кривая выше оси абсцисс Ох и является искомым графиком модульной рациональной или модульной дробно-рациональной функции левой части неравенства.

2. Найти точки пересечения графиков и выделить их выколотыми точками, если неравенство строгое, и закрашенными точками, если неравенство нестрогое.

3. На графике модульной функции выделить ту часть, которая расположена ниже прямой у = а, если в неравенстве модуль рационального или дробно-рационального выражения меньше или не больше числа а. Если в неравенстве стоит знак больше или не меньше, то на графике надо выделить часть графика, расположенную выше прямой у = а.

4. Решением исходного неравенства являются абсциссы точек выделенной части графика.

Рассмотрим примеры решения модульных рациональных и модульных дробно-рациональных неравенств с помощью графиков.

ПРИМЕР 1.

Решить неравенство |x3 – 6x2 +12x–12| < 4c помощью графиков.

РЕШЕНИЕ.

Решим модульное рациональное неравенство. 

Первый шаг. В одной системе координат построим график модульной рациональной функции у = |x3 – 6x2 +12x–12| и график линейной функции у = 4. Для удобства построения графика функции у = x3 – 6x2 +12x–12 преобразуем её. Так как запись рациональной функции состоит из суммы одночленов всех натуральных степеней не выше третьей и знаки одночленов чередуются, то попробуем представить её в виде куба разности. Вспомним формулу сокращённого умножения куб разности: (a– b)3 = a3 – 3a2b + 3ab2 – b3. Тогда функцию можно записать в виде у = х3 – 3·х2·2 + 3·х·22 – 23– 4 или 

у = (х – 2)3 – 4. Графиком этой кубической функции является кубическая парабола в новой системе координат с началом в точке с координатами (2; –4). Отобразим часть кубической параболы, расположенную ниже оси абсцисс Ох, в верхнюю полуплоскость относительно этой же оси. Полученная непрерывная кривая, расположенная в верхней полуплоскости, является графиком модульной кубической функции у = |x3 – 6x2 +12x–12|. Графиком линейной функции у = 4 является прямая, параллельная оси Ох и проходящая через точку с координатами (0; 4). 

Второй шаг. Отметим точки пересечения графиков модульной кубической функции и линейной функции выколотыми точками, так как в неравенстве стоит строгий знак меньше. 

Третий шаг. На графике модульной кубической функции выделим ту часть, которая расположена ниже прямой у = 4, так как в неравенстве стоит знак меньше. 

Четвертый шаг. Запишем в ответ множество значений абсцисс точек выделенной части графика. Получаем, что значения абсцисс всех точек модульной кубической функции, расположенных ниже прямой у = 4, находятся в интервале от 2 до 4. 

Ответ: х ∊ (2; 4).

ПРИМЕР 2.

РЕШЕНИЕ.

Решим модульное дробно-рациональное неравенство. 

Первый шаг. В одной системе координат построим график модульной дробно- 

Для этого числитель 2х – 4 распишем как 2х + 2 – 6 равное 2(х + 1) – 6. Затем полученное координат с началом в точке с координатами (–1; 2). Отобразим часть гиперболы, расположенную ниже оси абсцисс Ох, в верхнюю полуплоскость относительно этой же оси. Полученная непрерывная кривая, расположенная в верхней полуплоскости, является функции у = 4 является прямая, параллельная оси абсцисс Ох и проходящая через точку с координатами (0; 4). 

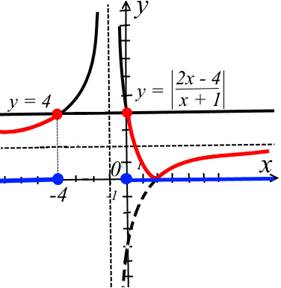
Второй шаг. Отметим точки пересечения графиков модульной дробно-рациональной функции и линейной функции закрашенными точками, так как в неравенстве стоит нестрогий знак. 

Третий шаг. На графике модульной дробно-рациональной функции выделим ту часть, которая расположена не выше прямой у = 4, так как в неравенстве стоит знак меньше или равно. 

Четвёртый шаг. Запишем в ответ множество значений абсцисс точек выделенной части графика. Получаем, что значения абсцисс всех точек модульной дробно-рациональной функции, расположенных не выше прямой у = 4, не больше –4 и не меньше 0. 

Ответ: х ∊ (– ∞; –4]∪ [0; +∞).