
На этом занятии мы дадим аналитическое определение модуля и модульного рационального и дробно-рационального неравенства, а также рассмотрим аналитический способ решения таких неравенств.
Модульным рациональным неравенством называется неравенство вида |f (x)| < с, где c – число, f(х) – рациональное выражение, иначе говорят, многочлен.
Заметим, что линейное выражение f(x) = ах + b является многочленом 1-й степени, значит, оно является частным случаем множества всех рациональных выражений. Модульным дробно-рациональным неравенством называется неравенство вида модуль p(x), делённое на q(x), меньше 0
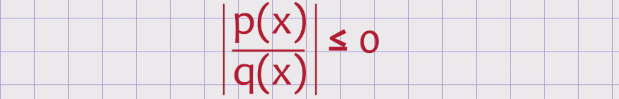
При этом в неравенствах может стоять не только знак меньше <, но и знак больше >, не меньше ≥ или не больше ≤. Существует два основных способа решения модульного рационального и дробно-рационального неравенств: аналитический и функционально-графический. Выбор способа решения зависит от используемого определения модуля. Разберём алгоритм решения модульных рационального и дробно-рационального неравенств с помощью аналитического определения модуля, то есть с помощью раскрытия модульных скобок. Аналитическое определение модуля: модулем числа а называется само число а, если оно неотрицательное и противоположное числу а, если оно отрицательное.

Подмодульное выражение f(x) и p(x), делённое на q(x), может принимать как неотрицательное, так и отрицательное значения. Согласно аналитическому определению, если оно положительное или ноль, то при раскрытии скобок знак неравенства не меняется, то есть получаем рациональное f(х) < с и дробно-рациональное неравенства р(х), делённое на q(x), < c, а если оно отрицательное, то при раскрытии скобок знак неравенства меняется на противоположный, то есть получаем рациональное f(x) > – c и дробно-рациональное неравенства р(х), делённое на q(x), > – c. При этом надо помнить, что рациональное модульное f(x) по модулю |f(x)| < с и дробно-рациональное неравенства р(х), делённое на q(x), по модулю:

со знаком меньше или не больше |f(x)| ≤ с

заменяется равносильной системой рациональных неравенств f(x) < с и f(x) > – c и дробно-рациональных неравенств р(х), делённое на q(x), < c и р(х), делённое на q(x),> –c
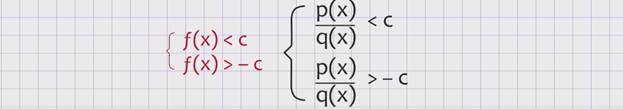
или f(x) ≤ с и f(x) ≥ –c в рациональном модульном неравенстве и р(х), делённое на q(x), не больше c и р(х), делённое на q(x), не меньше –c в дробно-рациональном модульном неравенств:
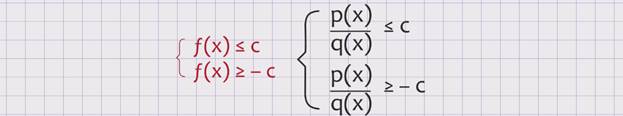
Для всех только положительных значений с в строгом неравенстве и неотрицательных значений с в нестрогом. В случае отрицательного значения с модульное неравенство не имеет решений. Если с равно 0, то модульное строгое неравенство также не имеет решений, а нестрогое заменяется равносильным уравнением подмодульное выражение равно 0.
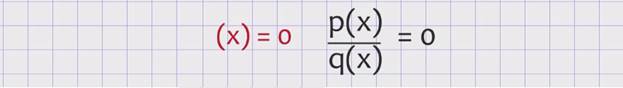
Решением системы неравенств будет множество чисел, удовлетворяющих каждому неравенству системы. Если же рациональное и дробно-рациональное модульное неравенство имеет знак больше.
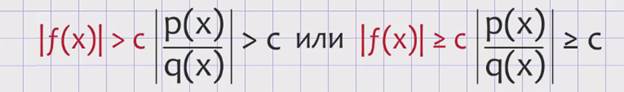
то оно заменяется равносильной совокупностью рациональных неравенств:
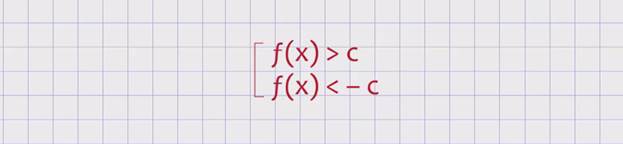
и дробно-рациональных неравенств р(х), делённое на q(x), больше c и р(х), делённое на q(x), меньше –c
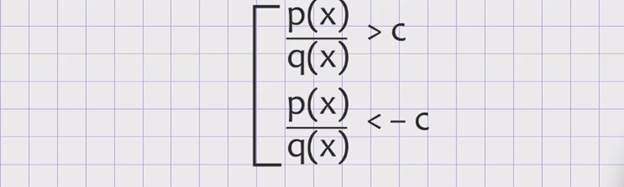
или f(x) ≥ с и f(x) ≤ –c в нестрогих рациональных неравенствах и р(х), делённое на q(x), не больше c и р(х), делённое на q(x), не меньше –c в нестрогих дробно-рациональных неравенствах для всех положительных значений с.
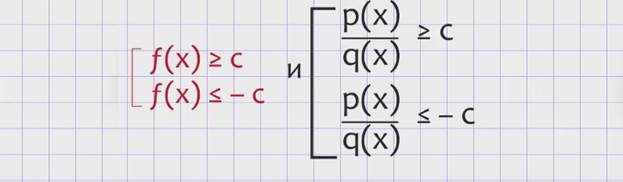
Если с меньше или равно 0 с ≤ 0, то решением модульного неравенства является любое число. Решением совокупности неравенств будет множество чисел, удовлетворяющих хотя бы одному неравенству совокупности. Рассмотрим примеры решения модульных рациональных и дробно-рациональных неравенств аналитическим способом.
 Подпишись и будь
в курсе новых событий и новостей!
Подпишись и будь
в курсе новых событий и новостей!