Модульным линейным неравенством называется неравенство вида|ax + b| < с, где а, b, c - числа, х - переменная. При этом в неравенстве может стоять не только знак меньше < , но и знак больше >, не меньше ≥ или не больше ≤.

Существует два основных способа решения линейного неравенства: 

- аналитический,

- графический.

Выбор способа решения зависит от используемого определения модуля. 

Геометрическое определение модуля: модулем числа а называется расстояние на координатной прямой от начала отсчёта до точки а.

Разберём алгоритм решения линейного неравенства |ax + b| < с с помощью геометрического определения модуля, то есть с помощью координатной прямой. Согласно геометрическому определению модуля, расстоянием между точками х и р на координатной прямой является модуль разности чисел х и р. ρ(х;р) = |x – p|

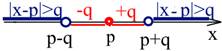
Строгое неравенство вида |x – p| > qопределяет условие, что расстояние между искомым значением х и точкой р на координатной прямой больше q. Решением такого неравенства является множество значений переменной х, меньших p– q и больших p + q. Геометрически эти решения моделируются в два открытых луча с выколотыми точками в их начале, расположенных слева от p– q и справа от p+q.

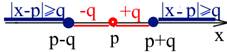
В нестрогом неравенстве |x – p| ≥ qрешением будут аналогичные промежутки, но с включёнными пограничными точками.

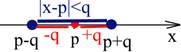
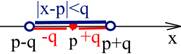
Строгое неравенство вида |x – p| < q определяет условие, что расстояние между искомым значением х и точкой р на координатной прямой меньше q. Решением такого неравенства является множество значений переменной х, больших p– q и меньших p + q. Геометрически эти решения моделируются в интервал с выколотыми точками на концах p – q и p+q.

В нестрогом неравенстве |x – p| ≤ qрешением будет отрезок от p– q до p+q с включёнными пограничными точками.