Рациональным неравенством называется неравенство вида f(x) < 0, где f(х) - многочлен
В этом неравенстве может стоять не только знак меньше (< ), но и знак больше ( >), не больше ( ≤ ) или не меньше ( ≥ ). Заметим, что линейный двучлен aх + b является частным случаем многочлена первой степени, а квадратный трёхчлен - частным случаем многочлена второй степени.
Рассмотрим схему решения рационального неравенства методом интервалов. Для этого надо:
1. найти нули левой части неравенства, то есть нули многочлена;
2. на числовой прямой отметить нули многочлена и промежутки его знакопостоянства, применив правило знакочередования. Здесь важно помнить, что, если неравенство строгое, то точки надо отметить выколотыми, а, если неравенство нестрогое, то точки надо отметить закрашенными.
Правило знакочередования заключается в следующем: крайний правый промежуток на числовой прямой имеет знак старшего коэффициента, который стоит перед переменной большей степени.
Далее, если нуль многочлена имеет нечётную кратность, то есть многочлен имеет нечётное число таких корней, то знак справа налево при переходе через этот нуль меняется на противоположный, а, если нуль многочлена имеет чётную кратность, то есть многочлен имеет чётное число таких корней, то знак справа налево при переходе через этот нуль сохраняется. Для удобства нули чётной кратности принято выделять петелькой;
3. на числовой прямой выделить промежутки, соответствующие знаку неравенства и записать ответ.
Рассмотрим примеры решения рациональных неравенств методом интервалов.
Пример 1. Решить неравенство (х – 2)(х + 3)4(5 – 2х)5 ≥ 0
РЕШЕНИЕ. Решим неравенство методом интервалов:
1. найдём нули многочлена левой части неравенства.
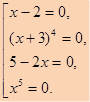
Для этого решим уравнение (х – 2)(х + 3)4(5 – 2х)5 = 0.
Известно, что произведение равно нулю, если хотя бы один из множителей равен нулю. Значит, решим совокупность уравнений х – 2 = 0; (х + 3)4 = 0;
5 – 2х = 0; х5 = 0. Получим корни х = 2; х = – 3 чётной кратности, х = 2,5;
х = 0 нечётной кратности.
2. на числовой прямой отметим найденные нули, причём число х = – 3 отметим петелькой в силу его чётной кратности.
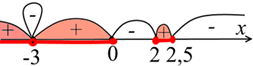
Неравенство содержит нестрогий знак, значит, точки отметим закрашенными кружочками. Определим знак старшего коэффициента многочлена. Для этого определим знак произведения старших коэффициентов каждого множителя в соответствующей степени. Так как, нам не важно знать числовое значение такого произведения, то при положительном знаке можно поставить 1, а при отрицательном – 1. Важно помнить, что в произведении знак перед многочленом тоже необходимо учитывать. В нашем многочлене имеем произведение 1 · 1 · 14 · (– 1) · 15= – 1. Получили отрицательный результат, следовательно, в крайний правый промежуток числовой прямой надо поставить знак « – ». Далее знаки чередуем справа налево, как показано на чертеже.
3. на числовой прямой выделим промежутки, содержащие знак « + », так как в неравенстве стоит знак больше или равно ( ≥). Точки выделенных промежутков и являются решением неравенства.
Ответ: х принадлежит лучу меньше нуля (< 0) и отрезку от 2 до 2,5.
Пример 2.Решить неравенство – (x + 1)х2 (4х + 3)3(4 - х)4 < 0
РЕШЕНИЕ. Решим неравенство методом интервалов.
1. найдём нули многочлена левой части неравенства.
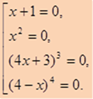
Для этого решим уравнение – (x + 1)х2(4х + 3)3(4 – х)4 = 0.
Известно, что произведение равно нулю, если хотя бы один из множителей равен нулю. Значит, решим совокупность уравнений х + 1 = 0; х2 = 0;
(4х + 3)3 = 0; (4 - х)4 = 0. Получим корни х = – 1; х = 0 чётной кратности, х = – 0,75 нечётной кратности, х = 4 чётной кратности.
2. на числовой прямой отметим найденные нули, причём числа х = 0 и х = 4 отметим петелькой в силу их чётной кратности. Неравенство содержит строгий знак, значит, точки отметим выколотыми кружочками. Определим знак старшего коэффициента многочлена. Для этого определим знак произведения старших коэффициентов каждого множителя в соответствующей степени. Так как, нам не важно знать числовое значение такого произведения, то при положительном знаке можно поставить 1, а при отрицательном – 1.
Важно помнить, что в произведении знак перед многочленом тоже необходимо учитывать. В нашем многочлене имеем произведение – 1 · 1 · 12 · 13 · (–1)4 = – 1. Получили отрицательный результат, следовательно, в крайний правый промежуток числовой прямой надо поставить знак « – ». Далее знаки чередуем справа налево, как показано на чертеже.
3. на числовой прямой выделим промежутки, содержащие знак « – », так как в неравенстве стоит знак меньше. Решением неравенства являются все числа из выделенных промежутков.
Ответ: х принадлежит открытым лучам меньше – 1 и больше 4, а также интервалам от
- 0,75 до нуля и от нуля до 4.
 Подпишись и будь
в курсе новых событий и новостей!
Подпишись и будь
в курсе новых событий и новостей!