В этом уроке познакомимся с правилами умножения и деления положительных и отрицательных чисел.

Известно, что любое произведение можно представить в виде суммы одинаковых слагаемых.

Cлагаемое -1 нужно сложить 6 раз:

(-1)+(-1)+(-1) +(-1) +(-1) + (-1) =-6

Значит произведение -1 и 6 равно -6.

Числа 6 и -6 –противоположные числа.

Таким образом, можно сделать вывод:

При умножении -1 на натуральное число получится противоположное ему число.

Для отрицательных чисел, так же как для положительных, выполняется переместительный закон умножения:

Если натуральное число умножить на -1, то также получится противоположное число

При умножении любого неотрицательного числа на 1 получится это же число.

Например:

Для отрицательных чисел данное утверждение тоже верно: -5 ∙1 = -5; -2 ∙ 1 = -2.

Вывод:

При умножении любого числа на 1 получится это же число.

Мы уже убедились, что при умножении минус 1 на натуральное число получится противоположное ему число. При умножении отрицательного числа данное утверждение тоже справедливо.

Например: (-1) ∙ (-4) = 4.

Также -1 ∙ 0 = 0, число 0 противоположно само себе.

Вывод:

При умножении любого числа на минус 1 получится противоположное ему число. 

Перейдем к другим случаям умножения. Найдем произведение чисел -3 и 7.

Отрицательный множитель -3 можно заменить произведением -1 и 3. Тогда можно применить сочетательный закон умножения:

3 ∙ 7 = 21

-1 ∙ 21 = -21, т.е. произведение минус 3 и 7 равно минус 21.

Вывод:

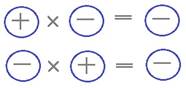
При умножении двух чисел с разными знаками получается отрицательное число, модуль которого равен произведению модулей множителей.

А чему равно произведение чисел с одинаковыми знаками?

Мы знаем, что при умножении двух положительных чисел получится положительное число. Найдем произведение двух отрицательных чисел.

Заменим один из множителей произведением с множителем минус 1.

Применим выведенное нами правило, при умножении двух чисел с разными знаками получается отрицательное число, модуль которого равен произведению модулей множителей,

получится -80.

Сформулируем правило:

При умножении двух чисел с одинаковыми знаками получается положительное число, модуль которого равен произведению модулей множителей.

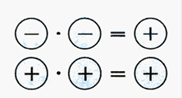
Перейдем к делению.

Подбором найдем корни следующих уравнений:

y ∙ (-2) = 10. 5 ∙ 2 = 10, значит х = 5; 5 ∙ (-2) = -10, значит а = 5; -5 ∙ (-2) = 10, значит y = -5.

Запишем решения уравнений. В каждом уравнении неизвестен множитель. Неизвестный множитель находим, разделив произведение на известный множитель, значения неизвестных множителей мы уже подобрали.

Проанализируем.

При делении чисел с одинаковыми знаками (а это первое и второе уравнения) получается положительное число, модуль которого равен частному модулей делимого и делителя.

При делении чисел с разными знаками (это третье уравнение) получается отрицательное число, модуль которого равен частному модулей делимого и делителя. Т.е. при делении положительных и отрицательных чисел знак частного определяется по тем же правилам, что знак произведения. А модуль частного равен частному модулей делимого и делителя.

Таким образом, мы сформулировали правила умножения и деления положительных и отрицательных чисел.