В этом уроке познакомимся с понятиями «система координат», «координатная плоскость», «оси координат», научимся строить точки на плоскости по координатам.

Возьмем координатную прямую х с началом координат точкой О, положительным направлением и единичным отрезком.

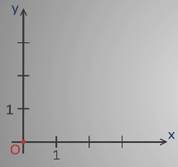
Через начало координат точку О координатной прямой х проведем еще одну координатную прямую y, перпендикулярную х, положительное направление зададим вверх, единичный отрезок такой же. Таким образом, мы построили систему координат.

Дадим определение:

Две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является началом координат каждой из них, образуют систему координат.

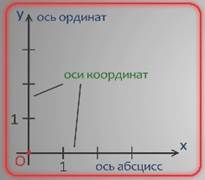
Прямые, которые образуют систему координат, называют координатными осями, каждая из которых имеет свое название: координатная прямая х – ось абсцисс, координатная прямая y – ось ординат.

Плоскость, на которой выбрана система координат, называется координатной плоскостью.

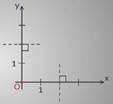
Описанная система координат называется прямоугольной. Часто ее называют декартовой системой координат в честь французского философа и математика Рене Декарта.

Каждая точка координатной плоскости имеет две координаты, которые можно определить, опустив из точки перпендикуляры на оси координат. Координаты точки на плоскости – это пара чисел, из которых первое число – абсцисса, второе число – ордината. Абсциссу показывает перпендикуляр к оси х, ординату – перпендикуляр к оси y.

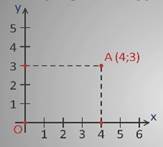
Отметим на координатной плоскости точку А, проведем из неё перпендикуляры к осям системы координат.

По перпендикуляру к оси абсцисс (ось х) определяем абсциссу точки А, она равна 4, ординату точки А – по перпендикуляру к оси ординат (ось у) – это 3. Координаты нашей точки 4 и 3. А (4;3). Таким образом, координаты можно найти для любой точки координатной плоскости.

А как построить точку на плоскости с заданными координатами, т.е. по координатам точки плоскости определить её положение? В данном случае действия выполняем в обратном порядке. На координатных осях находим точки соответствующие заданным координатам, через которые проводим прямые, перпендикулярные осям х и y. Точка пересечения перпендикуляров и будет искомой, т.е. точкой с заданными координатами.

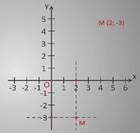
Выполним задание: построить на координатной плоскости точку М (2;-3).

Для этого на оси абсцисс находим точку с координатой 2, проводим через данную точку прямую перпендикулярную оси х. На оси ординат найдем точку с координатой -3, через нее проведем прямую перпендикулярную оси y. Точка пересечения перпендикулярных прямых и будет заданной точкой М.

А теперь рассмотрим несколько частных случаев.

Отметим на координатной плоскости точки А (0; 2), В (0; -3), С (0; 4).

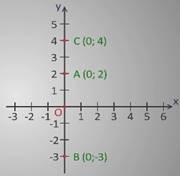
Абсциссы данных точек равны 0. На рисунке видно, что все точки находятся на оси ординат.

Следовательно, точки, абсциссы которых равны нулю, лежат на оси ординат.

Поменяем координаты данных точек местами.

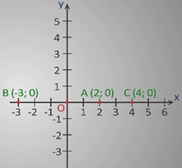
Получится А (2;0), В (-3;0) С (4; 0). В этом случае все ординаты равны 0 и точки находятся на оси абсцисс.

Значит, точки, ординаты которых равны нулю, лежат на оси абсцисс.

Разберем еще два случая.

На координатной плоскости отметим точки М (3; 2), N (3; -1), Р (3; -4).

Легко заметить, что все абсциссы точек одинаковые. Если эти точки соединить, получится прямая, параллельная оси ординат и перпендикулярная оси абсцисс.

Напрашивается вывод: точки, имеющие одну и ту же абсциссу, лежат на одной прямой, которая параллельна оси ординат и перпендикулярна оси абсцисс.

Если поменять координаты точек М, N, Р местами, то получится М (2; 3), N (-1; 3), Р (-4; 3). Одинаковыми станут ординаты точек. В данном случае, если эти точки соединить, получится прямая параллельная оси абсцисс и перпендикулярная оси ординат.

Таким образом, точки, имеющие одну и ту же ординату, лежат на одной прямой параллельной оси абсцисс и перпендикулярной оси ординат.

В этом уроке Вы познакомились с понятиями «система координат», «координатная плоскость», «оси координат - ось абсцисс и ось ординат». Узнали, как найти координаты точки на координатной плоскости и научились строить точки на плоскости по ее координатам.