В этом уроке выведем правила умножения и деления обыкновенных дробей.
Рассмотрим задачу:
![]()
Чтобы найти площадь прямоугольника, нужно его длину умножить на ширину.
![]()
![]()
![]()
![]()
Они отличаются первыми множителями, вторые множители у них одинаковые.
![]()
Значит, числовое выражение справа будет отличаться от левого тем, что первый его множитель в 13 раз меньше первого множителя в выражении слева.
Тогда и произведение должно быть в 13 раз меньше.
Таким образом, чтобы найти площадь второго прямоугольника, нужно площадь первого прямоугольника разделить на 13.
![]()
![]()
![]()
Проанализируем:
![]()
![]()
Следовательно, чтобы умножить одну обыкновенную дробь на другую, нужно числитель первой дроби умножить на числитель второй дроби, получится числитель произведения; знаменатель первой дроби умножить на знаменатель второй дроби, получится знаменатель произведения.
![]()
Таким образом, произведение обыкновенных дробей – это дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей данных дробей.
Иногда в задачах нужно умножать и смешанные числа.
![]()
Смешанное число – это число, которое состоит из двух частей: целой и дробной.
Для того чтобы выполнить умножение, смешанные числа необходимо представить в виде неправильных дробей: и далее выполнить умножение по правилу умножения обыкновенных дробей.
![]()
15 умножаем на 9, получится 135 – это числитель
7 умножаем на 2, получится 14 – это знаменатель
![]()
Перейдем к делению обыкновенных дробей.
Рассмотрим задачу:
![]()
![]()
Вспомним, как выполнить деление обыкновенной дроби на натуральное число:
надо знаменатель умножить на число, а числитель остается таким же.
![]()
Изменим условие задачи:
![]()
![]()
Вспомним, что при делении натурального числа на десятичную дробь мы заменяем дробь натуральным числом, переносим запятые в делимом и делителе на столько знаков, чтобы делитель стал натуральным числом.
Попробуем применить этот способ с обыкновенными дробями.
![]()
![]()
![]()
Умножим дроби на число.
![]()
![]()
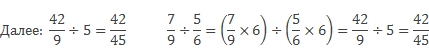
Числитель частного 42 – это произведение числителя первой дроби 7 и знаменателя второй дроби 6, знаменатель частного – это произведение знаменателя первой дроби 9 и числителя второй дроби 5.
Значит, числитель частного – это произведение числителя делимого и знаменателя делителя, а знаменатель – произведение знаменателя делимого и числителя делителя.
Вывод:
Чтобы разделить обыкновенную дробь на обыкновенную дробь, нужно числитель первой дроби умножить на знаменатель второй дроби, получится числитель частного; знаменатель первой дроби умножить на числитель второй дроби, получится знаменатель частного.
Сформулируем правило деления обыкновенных дробей по-другому.
![]()
При умножении числителей и знаменателей этих дробей получится одинаковый результат 30,
![]()
Если числитель и знаменатель дроби равны, то дробь равна 1.
Таким образом, перед нами числа, произведение которых равно 1, их называются взаимно обратными.
![]()
![]()
![]()
Результаты одинаковые. А значит можно сделать вывод:
Чтобы разделить число на обыкновенную дробь, нужно это число умножить на дробь обратную делителю.
Таким образом, в этом уроке Вы познакомились с правилами умножения и деления обыкновенных дробей.
 Подпишись и будь
в курсе новых событий и новостей!
Подпишись и будь
в курсе новых событий и новостей!