Подумаем, сколько трехзначных чисел можно составить из цифр 0, 1, 2 при условии, что цифры в числе не должны повторятся? Чтобы решить такую задачу, нужно перебрать все возможные варианты сочетания цифр или, говорят, «комбинации».

Комбинация в переводе с латинского обозначает сочетание, соединение. В математике комбинация – это набор или сочетание элементов, выбранных из данного множества.

Комбинаторика – раздел математики, который изучает, сколько различных комбинаций, подчиненных определенным условиям, можно составить из заданных объектов

Задачи, которые решаются путем перебора всех возможных комбинаций (вариантов), называются комбинаторными. Такие задачи часто встречаются в жизни.

Для решения задачи построим дерево возможных вариантов. Первая цифра в числе может быть 1 или 2. Если первая 1, то вторая может быть 0, или 2. Если первая 2,то вторая может быть 0 или 1. Если первая 1, вторая 0, то третья 2. Если первая 1,вторая 2, то третья 0. Если первая 2, вторая 0, то третья 1. Если первая 2, вторая 1, то третья 0.

Таким образом, получилось четыре комбинации:102, 120, 201, 210.

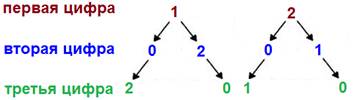
Дерево возможных вариантов можно назвать геометрической моделью рассматриваемой ситуации.

Эту же задачу можно решить по-другому, используя логические рассуждения и здравый смысл. А именно, первая цифра может быть 1 или 2 (2 варианта), для второй цифры остается тоже по два варианта, а для третьей – по одному, так как по условию цифры не должны повторяться, то есть 2 ∙ 2 ∙ 1 = 4, получается четыре варианта комбинаций.

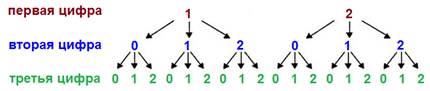
Изменим условие. Пусть цифры могут повторяться. Тогда вариантов будет больше. Первая цифра может быть 1 или 2. От каждой первой цифры теперь будет отходить три веточки. И от каждой второй тоже три веточки. Получается 18 вариантов. Комбинации100, 101, 102, 110, 111, 112, 120, 121, 122,

200, 201, 202, 210, 211, 212, 220, 221, 222.

Решим задачу вторым способом. Для первой цифры 2 варианта (1 или 2), для второй по три на каждую первую цифру, для третьей по три на каждую вторую, значит 2 ∙ 3 ∙ 3 = 18. Про второй способ рассуждения говорят, что мы использовали правило умножения для комбинаторных задач. Это аналитическая модель рассматриваемой ситуации.

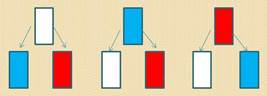
Используя правило умножения, решим еще одну задачу. В детском лагере ребята решили придумать флаг своего отряда. У них ткань белого, красного и синего цвета. Флаг должен быть двуцветным. Сколько вариантов флагов может быть?

Для первой полосы может быть 3 варианта, для второй тогда останется по 2 варианта:

3 ∙ 2 = 6 (флагов).

Заметим, что правило умножения применяется только, если дерево возможных вариантов правильное, то есть из каждого узла одного уровня выходит одно и то же число веток. Чтобы определить, правильное ли дерево, нет необходимости строить все дерево, достаточно выстроить один фрагмент.

Задача 1: От деревни до озера ведет 8 троп, туристы решили сходить к озеру, но вернуться по тропе, по которой не ходили. Сколько вариантов похода туристов возможно? Построим фрагмент дерева возможных вариантов. Если туристы пойдут по первой тропе, у них 7 вариантов вернуться обратно. Заметим, что для каждой следующей тропы тоже 7 вариантов возвращения. В данном случае, если чертить все дерево, то оно будет занимать много места, да и нет такой необходимости. По одному фрагменту можно определить, что дерево получится правильным, значит можно использовать правило умножения: 8 вариантов пути к озеру, на каждый 7 вариантов возвращения: 8 ∙ 7 = 56, получается 56 вариантов.

Правило умножения удобно использовать, когда количество вариантов достаточно большое, что затрудняет построение дерева возможных вариантов.

Задача 2: 4 друга при встрече обменялись рукопожатиями. Сколько всего было рукопожатий? В этой задаче обозначим друзей числами 1, 2, 3, 4.

Обозначение предметов, объектов условными знаками (числами, буквами) называется кодированием.

Понятно, что каждый друг не может пожать руку сам себе. Если первый пожмет руку второму, третьему и четвертому, то второму, третьему и четвертому уже не надо жать руку первому, у них вариантов остается меньше. Если второй пожмет руку третьему и четвертому, то третьему остается только пожать руку четвертому, а у четвертого совсем нет вариантов, потому, как со всеми он уже обменялся рукопожатиями. В данной задаче дерево не будет правильным. А количество вариантов можно найти не умножением, а сложением: у первого 3 варианта, у второго 2, у третьего 1,у четвертого 0, тогда 3 + 2 + 1 + 0 = 6 вариантов рукопожатий, причем каждый сделает три рукопожатия.