В этом уроке познакомимся с понятиями «луч», «открытый луч», «отрезок», «интервал», «числовые промежутки», а также научимся записывать по рисунку числовые промежутки и неравенства.

Для рассмотрения новых понятий воспользуемся рисунками, на которых изображена координатная прямая. Правда, без обозначенных на ней начала отсчета и единичного отрезка. Мы это сделали для того, чтобы не загромождать рисунок.

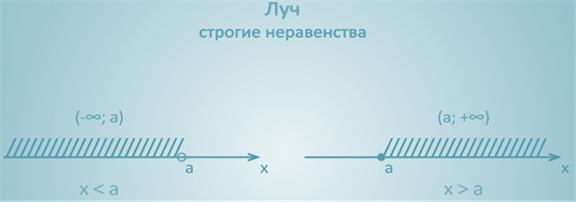
На координатной прямой отмечена точка a, штриховкой отмечены все точки прямой, которые лежат правее a,т.е. числа большие числаa.

Такое множество точек (чисел) называют открытым лучом и обозначают так:

Читают так: а плюс бесконечность или от а до плюс бесконечности.

Для любого числа х из этого множества верно неравенство х > a.

Таким образом, открытый луч – это луч, начало которого ему не принадлежит.

Рассмотрим еще один открытый луч:

На координатной прямой штриховкой отмечены точки, которые расположены слева от точки а. Эти числа меньше, чем а.

Данное множество точек (чисел) обозначается так:

И читается: от минус бесконечности до а.

Для любого числа х этого открытого луча верно неравенство

Обратите внимание, на рисунках, которые мы рассмотрели, точка, соответствующая числу а, обозначена незакрашенным кружочком.

Если закрасить кружок, то множество чисел изменится.

В этом случае число, обозначающее точку а, тоже принадлежит к заштрихованному множеству. Получается луч.

Данные множества записываются с помощью квадратной скобки:

Такие неравенства называют нестрогими.

Неравенства вида х > a и х < a называются строгими.

Рассмотрим еще два рисунка.

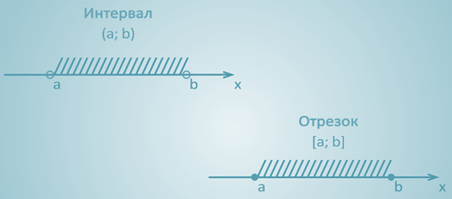
На обоих рисунках штриховкой обозначены точки (числа), которые находятся между точками a и b. В первом случае числа a и b не входят в множество – точки не закрашены, во втором входят – точки закрашены.

Первое множество называют интервалом и обозначают с помощью круглых скобок (a; b).

На втором рисунке изображен тот же интервал, но к нему присоединили его концы точки а и b, поэтому это уже не интервал, а отрезок, и записывается данное множество с помощью квадратных скобок [а; b].

Для всех точек интервала (a; b) верно двойное неравенство а < x < b, читается так: х больше а, но меньше b. Это строгое неравенство.

Для всех точек х, принадлежащих отрезку [а; b], верно двойное нестрогое неравенство а ≤ х ≤ b, (х больше или равен а, но меньше или равен b).

«Луч», «открытый луч», «отрезок», «интервал» – это всё числовые промежутки.

Часто при решении задачи мы рисуем схему по ее условию, а затем составляем уравнение. И схема и уравнение – это математические модели ситуации, описанной в задаче.

Схема – графическая модель, уравнение – аналитическая модель.

Аналогично дело обстоит и с числовыми промежутками.

Числовой промежуток – это все числа, соответствующие определенному условию.

Условие соответствует какой-либо математической ситуации. Можно построить как графическую, так и аналитическую модель, кроме того сделать еще и символическую запись.

Например, все числа меньшие 3.

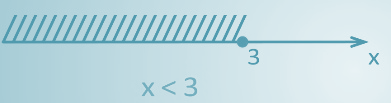
В данном случае числовым промежутком будет открытый луч, графическая модель будет такая:

Аналитической моделью является строгое неравенство х < 3, а символическая запись (-∞; 3).

Графическими моделями для числовых промежутков являются: луч, открытый луч, отрезок, интервал.

Аналитическими моделями: строгие, нестрогие неравенства, а так же двойные неравенства.

Итак, в этом уроке Вы познакомились с понятиями открытый луч, луч, отрезок, интервал, числовые промежутки и научились записывать числовые промежутки и неравенства по рисункам.