Рассмотрим алгоритм письменного вычитания многозначных чисел. Например, нам нужно найти значение разности чисел 397.539 и 25.128.
1. Прочитаем их. Уменьшаемое – 397.539, вычитаемое – 25.128.
2. Определяем количество разрядов в каждом числе. Это шестизначное и пятизначное числа.
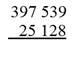
3. Записываем числа одно под другим так, чтобы единицы одинаковых разрядов находились в одном столбце.
Вычитаем разрядные единицы, начиная с самого первого разряда – единиц, заканчивая последним разрядом – десятки тысяч.
9 единиц минус 8, получится 1.
3 разрядных десятка уменьшится на 2 разрядных десятка, будет также 1.
Вычитаем разрядные сотни. 5 минус 1, получится 4.
В классе тысяч из 7 единиц тысяч вычитаем 5 единиц тысяч, получаем 2.
В последнюю очередь вычитаем десятки тысяч. Девять минус два, равно семи.
Разрядные сотни тысяч остаются без изменения.
4. Читаем ответ. Это шестизначное число 372.411.
Рассмотрим алгоритм вычитания из трёхзначных чисел. Нужно вспомнить разрядный состав числа. Например, нам необходимо из 750 вычесть 6. Представим уменьшаемое в виде суммы разрядных слагаемых: 750=700+50
Всегда должно соблюдаться правило: действия выполняются с единицами одинаковых разрядов, начиная с наименьшего. Из нуля вычесть 6 нельзя, поэтому уменьшаемое можно представить в виде суммы разрядных слагаемых так:
750=700+(40+10)
Из 5-ти десятков мы занимаем один десяток, затем из этого десятка вычитаем 6 и получаем 4. Значение разности равно 700+40+4=744.

Попробуем сделать запись данного действия вычитания в столбик. При вычитании разрядных единиц мы занимали один разрядный десяток. Чтобы об этом не забыть, поставим над цифрой 5 точку на строке памяти. При вычитании разрядных десятков точка напомнит нам о том, что осталось только 4 разрядных десятка. Таким образом, точка на строке памяти ставится, если невозможно выполнить вычитание без единиц большего разряда.
Рассмотрим вычитание многозначных чисел с переходом в следующий разряд.
Уменьшаемое – 290.380, вычитаемое – 37.161. Это шестизначное и пятизначное числа.
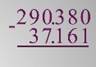
Записываем числа одно под другим так, чтобы единицы одинаковых разрядов находились в одном столбце.
Вычитаем разрядные единицы, начиная с самого первого разряда – единиц, заканчиваем последним разрядом – десятки тысяч.
Из 0 вычесть 1 нельзя, занимаем один разрядный десяток, а чтобы не забыть, ставим точку на строку памяти над разрядом десятков. Из 10 вычесть 1, получится 9 разрядных единиц. Точка напоминает нам о том, что разрядных десятков осталось 7. 7 минус 6, получится 1.
Вычитаем разрядные сотни. 3 минус 1, будет 2.
В уменьшаемом в разряде единиц тысяч стоит 0. Это значит, нам нужно занять один десяток тысяч. Чтобы запомнить, ставим точку на строке памяти и из 10 вычитаем 7. Получится 3 разрядных единицы тысяч.
В разрядных десятках тысяч с учётом отметки точкой, получается8. 8 минус 3, будет 5. Разрядные сотни тысяч остаются без изменения.
Читаем ответ: значение частного – шестизначное число 253.219.
Таким образом, письменное вычитание многозначных чисел выполняется в столбик по определённым правилам:
Во-первых, записывать числа необходимо одно под другим так, чтобы единицы одинаковых разрядов находились в одном столбце.
Во-вторых, вычитать разрядные единицы, начиная с самого первого разряда – единиц, заканчивая последним разрядом в классе тысяч.
В-третьих, в случае невозможности вычитания разрядных единиц без использования единиц большего разряда на строке памяти ставится точка.
 Подпишись и будь
в курсе новых событий и новостей!
Подпишись и будь
в курсе новых событий и новостей!