В алгебре часто при упрощении выражений и различных вычислениях используются переместительный и сочетательный законы.

Эти законы также справедливы для векторов.

Вспомним правило сложения векторов – правило треугольника.

Пусть нам даны два вектора а и b.

От произвольно выбранной точки А отложим вектор АВ, равный вектору а.

Затем от точки В отложим вектор ВС, равный вектору b.

Вектор АС называется суммой векторов а и b.

Воспользуемся этим правилом треугольника для доказательства следующей теоремы.

Теорема:

Для любых векторов а , b и с справедливы равенства:

сумма векторов а и b равна сумме векторов b и а (переместительный закон);

сумма векторов а плюс b и с равна сумме векторов а и b плюс с (сочетательный закон).

Для доказательства переместительного закона рассмотрим случай, когда векторы а и b не коллинеарны, т.е. ненулевые и не лежат на одной или параллельных прямых (случай коллинеарных векторов рассмотрите самостоятельно).

От произвольной точки А отложим вектор АВ, равный вектору а, и вектор АD, равный вектору b.

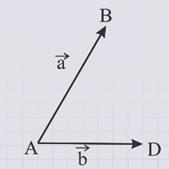
Основываясь на построенных векторах, достроим параллелограмм АВСD так, что вектор АВ равен вектору DС, а вектор АD равен вектору ВС.

По правилу треугольника сумма векторов АВ и ВС равна вектору АС, т.е. равна сумме векторов а и b.

С другой стороны, сумма векторов AD и DC также равна вектору АС, т.е. сумме векторов b и а.

Таким образом, сумма векторов а и b равна сумме векторов b и а.

Переместительный закон доказан.

Для доказательства сочетательного закона отложим от произвольной точки А вектор АВ, равный вектору а, от точки В вектор ВС, равный вектору b, и от точки С вектор CD, равный вектору с.

Рассмотрим сумму векторов а плюс b и вектора с с точки зрения правила треугольника: сумма векторов а и b равна вектору АС, в свою очередь, сумма вектора АС и вектора с равна вектору АD.

Теперь рассмотрим сумму векторов а и b плюс с: сумма векторов b и с, согласно рисунку, равна вектору ВD, в свою очередь, сумма векторов а и ВD равна вектору АD. 

Исходя из этого, сумма векторов а плюс b и с равна сумме векторов а и b плюс с.

Что доказывает сочетательный закон. 

Теорема доказана.

Важно отметить, что при доказательстве переместительного закона было обосновано правило параллелограмма сложения неколлинеарных векторов: чтобы сложить неколлинеарные векторы а и b, необходимо от произвольной точки А отложить вектор АВ, равный вектору а, и вектор AD, равный вектору b, затем достроить параллелограмм АВСD, тогда вектор АС равен сумме векторов а и b.

Правило треугольника и правило параллелограмма находят сумму двух векторов, но как сложить несколько векторов?

Чтобы сложить несколько векторов, необходимо сложить первый вектор со вторым, затем сложить их сумму с третьим вектором и так далее.

Из законов сложения векторов следует, что сумма нескольких векторов не зависит от того, в каком порядке происходит сложение.

Рассмотрим рисунок, отражающий сумму векторов а, b и с:

от произвольной точки А отложен вектор АВ, равный вектору а, затем от точки В отложен вектор ВС, равный вектору b, и, наконец, от точки С отложен вектор CD, равный вектору с.

В результате получается вектор АD, равный сумме векторов а, b и с.

Если продолжить процесс откладывания векторов, можно построить сумму четырех, пяти, любого количества векторов.

Правило построения суммы нескольких векторов называется правилом многоугольника: если А1, А2, …,Аn – произвольные точки плоскости, то сумма векторов А1А2, А2А3, …, Аn –1An равна вектору А1Аn.

Это равенство справедливо для всех точек А1, А2, …, Аn, в частности, когда некоторые из них совпадают.

Важно заметить, что если начало первого вектора совпадает с концом последнего вектора, то сумма данных векторов равна нулевому вектору.

Итак, подведем итоги: 

– Для любых векторов а, b и с справедливы равенства: 

сумма векторов а и b равна сумме векторов b и а; 

сумма векторов а плюс b и с равна сумме векторов а и b плюс с. 

– Чтобы сложить неколлинеарные векторы а и b, необходимо от точки А отложить вектор АВ, равный вектору а, и вектор AD, равный вектору b, затем достроить параллелограмм АВСD, тогда вектор АС равен сумме векторов а и b (правило параллелограмма).

– Если А1, А2 … An – произвольные точки плоскости, то сумма векторов 

А1А2, А2А3,.., Аn–1An равна вектору А1Аn (правило многоугольника).