В геометрии очень часто мы пользуемся отрезками различной длины.

Отрезок – это часть прямой, ограниченная двумя точками.

Можно ли назвать эти точки началом и концом отрезка?

Ответом на этот вопрос будет определение, что такое вектор.

Однако для того, что бы дать это определение, рассмотрим отрезок более подробно.

Произвольный отрезок имеет два конца.

Концы отрезка также называют граничными точками.

На отрезке можно указать два направления: от одной граничной точки к другой и наоборот.

Чтобы выбрать одно из этих направлений, одну граничную точку отрезка назовём началом отрезка, а другую – концом отрезка и будем считать, что отрезок направлен от начала к концу.

Таким образом, отрезок, для которого указано, какая из его граничных точек считается началом, а какая – концом, называется направленным отрезком или вектором.

На рисунках вектор изображается отрезком со стрелкой, показывающей направление вектора. Векторы обозначают двумя заглавными буквами со стрелкой над ними.

Первая буква – начало вектора, вторая – конец. Также вектор может обозначаться и одной строчной латинской буквой.

Кроме отрезка, вектором может быть любая точка плоскости.

В этом случае вектор называется нулевым.

Начало нулевого вектора совпадает с его концом.

Например, на плоскости выбрана точка М, тогда нулевой вектор в этой точке будет обозначен как:

Нулевой вектор также обозначается символом, отображающим цифру ноль со стрелочкой над ним:

Теперь рассмотрим понятие длины вектора.

Рассмотрим два вектора АВ и СD, расположенные на одной прямой.

Эти векторы могут быть направлены либо в одну и ту же сторону, либо их направление противоположно. Данные ненулевые векторы, расположенные на одной или параллельных прямых, называются коллинеарными.

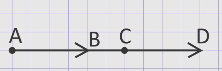
Нулевой вектор считается коллинеарным любому вектору.

Коллинеарные векторы обладают рядом свойств.

Рассмотрим три ненулевых коллинеарных вектора а, в, и с.

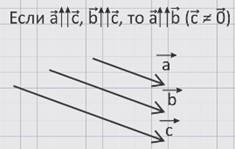
Первое свойство:

Если вектор а сонаправлен с вектором с и вектор в сонаправлен с вектором с, то векторы а и в также имеют одно направление – данное утверждение является первым свойством коллинеарных векторов.

Второе свойство:

Если вектор а противоположно направлен вектору с и вектор в противоположно направлен вектору с, то векторы а и в сонаправленные.

Третье свойство:

Коллинеарных векторов говорит о том, что если векторы а и с сонаправлены, а вектор в противоположно направлен с вектором с, то векторы а и в противоположно направленные.

Итак, подведем итоги урока: 

Вектор – это отрезок, для которого указано, какая из его граничных точек считается началом, а какая – концом. Векторы обозначают двумя заглавными буквами со стрелкой над ними. Любую точку плоскости можно считать нулевым вектором. Длиной вектора называется длина соответствующего отрезка; ненулевые векторы, которые лежат на одной прямой или параллельных прямых, называются коллинеарными. Если два вектора сонаправлены и их длины равны, то такие векторы называются равными.