Задачи на построения занимают отдельное место среди задач разделов геометрии. Откладывание вектора от данной точки – первая задача на построение раздела «Векторы».

Рассмотрим вектор а.

Пусть начало этого вектора будет точка А, а конец – точка В.

Говорят, что вектор а отложен от точки А.

Если ненулевые векторы АВ и СD, расположенные на одной или параллельных прямых, направлены в одну и ту же сторону,

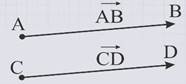
то они называются сонаправленными и обозначаются так:

Докажем следующее утверждение:

от любой точки М можно отложить вектор, равный данному вектору а, и притом только один.

Предположим, что данный вектор а нулевой.

Так как любую точку плоскости можно считать нулевым вектором, то искомым вектором является нулевой вектор ММ – любая точка М плоскости. 

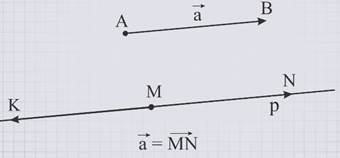
Пусть данный вектор не нулевой, тогда пусть он имеет начало в точке А и конец в точке В. Проведем через точку М прямую p, параллельную данному вектору АВ.

От точки М возможно отложить два отрезка МN и MK, равные отрезку АВ.

Из векторов МN и MK только вектор MN сонаправлен с вектором АВ, этот вектор и является равным данному вектору а.

По построению такой вектор единственный.

На самом деле предположим, что через точку М возможно провести два вектора, равных данному, например, вектор MN и MN1.

Но тогда они оба будут сонаправлены с данным вектором а, следовательно, будут либо лежать на одной прямой, т.е. полностью совпадать, либо находиться на параллельных прямых.

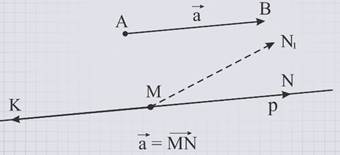
Но векторы МN и MN1 не могут лежать на параллельных прямых, так как имеют общую точку М.

Таким образом, наше предположение неверно, и от точки М можно отложить вектор, равный данному, и притом только один.

Необходимо заметить, что равные векторы, отложенные от разных точек, часто обозначают одной и той же буквой.

Иногда про такие векторы говорят, что это один и тот же вектор, но отложенный от разных точек.