На первый взгляд может показаться, что векторы и связанные с ними понятия мало применимы к решению различного рода задач в геометрии. Однако использование свойств векторов помогает решить определенные задачи и доказать некоторые теоремы более быстрым способом.

Рассмотрим задачу: точка С – середина отрезка АВ. Точка М – любая точка плоскости. Доказать, что

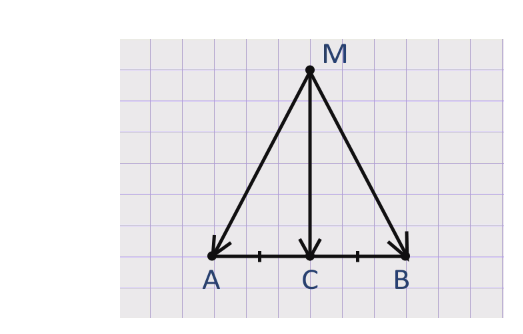
При доказательстве используем правило треугольника, получим следующие равенства:

Складывая данные равенства, получим:

Так как точка С – середина отрезка АВ, то сумма

= тогда

или

Что и требовалось доказать.

Рассмотрим ещё одну задачу.

Необходимо доказать, что прямая, проведенная через середины оснований трапеции, проходит через точку пересечения продолжений боковых сторон.

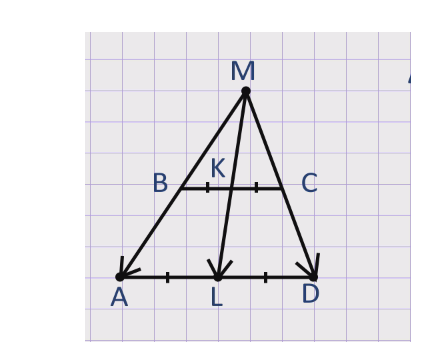
Итак, пусть нам дана трапеция ABCD с основаниями AD и ВС, точка К – середина стороны ВС, точка L – середина стороны AD и точка М пересечение прямых АВ и CD. Докажем, что точка М лежит на прямой KL.

Треугольник АМD подобен ∆ ВМС по первому признаку подобия треугольников, следовательно,

Поскольку векторы

Обозначим данные равенства цифрой 1. Так как точка К – середина стороны ВС и точка L – середина стороны АD, то

тогда, подставив в это равенство выражения под цифрой 1 для векторов

получим

Полученное равенство показывает, что векторы коллинеарны, то есть лежат либо на параллельных прямых, либо на одной прямой.

Поскольку рассмотренные векторы имеют общую точку, то они лежат на одной прямой, что в свою очередь доказывает, что точка М принадлежит прямой KL.