Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.
Число, равное отношению сходственных сторон подобных треугольников, называют коэффициентом подобия.
Для решения задач в геометрии часто используются три признака подобия треугольников, сформулируем второй из них.
Теорема: Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
Докажем это утверждение.
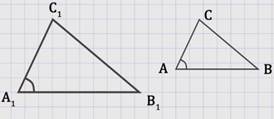
Дано:
![]()
Доказать:
∆ АВС и ∆ А1В1С1 подобны.
Доказательство:
Для доказательства применим первый признак подобия треугольников, а именно: «Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны» .
По условию ∠А = ∠А1 , остается доказать, что ∠В = ∠В1.
Рассмотрим ∆АВС2, у которого ∠1 = ∠А1, ∠2 = ∠В1.
∆ АВС2 и ∆ А1В1С1 подобны по первому признаку подобия треугольников, поэтому
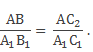
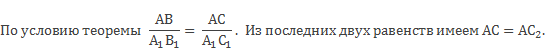
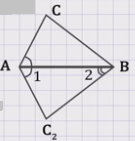
Рассмотрим ∆АВС и ∆АВС2.
Так как у этих треугольников,
во-первых, сторона АВ – общая,
во-вторых, АС = АС2,
в-третьих, ∠САВ = ∠1, так как ∠САВ = ∠А1и ∠1 = ∠А1 ,
можно сделать вывод, что ∆АВС = ∆АВС2 по двум сторонам и углу между ними.
Из равенства треугольников ∆АВС и ∆АВС2 следует, что ∠В = ∠2, а так как ∠2 = ∠В1 , то ∠В = ∠В1.
Что и требовалось доказать.
Решим задачу.
Задача: Отрезки АD и ВС пересекаются в точке О так, что АО = 12 см, ВО = 10 см, СО = 30 см, DО = 4 см. Докажите, что треугольники АОС и DОВ подобны.
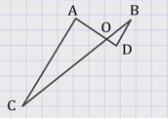
Решение:
Дано:
АD и ВС пересекаются в точке О.
АО = 12 см,
ВО = 10 см,
СО = 30 см,
DО = 4 см.
Доказать:
треугольники АОС и DОВ подобны.
Доказательство:
![]()
вертикальные углы), а значит, треугольники АОС и DОВ подобны по второму признаку подобия треугольников.
 Подпишись и будь
в курсе новых событий и новостей!
Подпишись и будь
в курсе новых событий и новостей!