В этом уроке познакомимся с первым признаком подобия треугольников, рассмотрим задачу на применение этого признака.

В начале урока вспомним следующее определение:

два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.

Сходственными называются стороны подобных треугольников, лежащие против равных углов. У подобных треугольников АВС и А1И1С1 сходственными сторонами являются АВ и А1В1, ВС и В1С1, АС и А1С1..

Докажем теорему, отражающую первый признак подобия треугольников:

Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

Дано:

∆АВС и ∆А1В1С1

∠А = ∠А1

∠В = ∠В1

Доказать:

∆АВС ~ ∆А1В1С1

Доказательство:

Докажем, что углы АВС соответственно равны углам ∆А1В1С1.

По условию теоремы ∠А = ∠А1, ∠В = ∠В1.

Остается доказать, что ∠С = ∠С1.

Для доказательства применим теорему о сумме углов треугольника.

∠С = 180° – (∠А + ∠ В)

∠С1 = 180° – (∠А1 + ∠В1)

Значит, ∠С = ∠С1.

Далее докажем, что стороны АВС пропорциональны сходственным сторонам ∆А1В1С1.

Так как ∠А = ∠А1 и ∠С = ∠С1, то применим теорему об отношении площадей треугольников, имеющих по равному углу, а именно:

А теперь перейдем к рассмотрению задачи.

Дано:

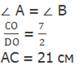
Найти:

ВD

Решение:

Рассмотрим ∆АОС и ∆ВОD.

Так как ∠А = ∠В (по условию задачи);

∠АОС =∠ ВОD (как вертикальные углы), то по первому признаку подобия треугольников ∆АОС ~ ∆ВОD.

Ответ: 6 см.