В этом уроке познакомимся с понятием «средняя линия треугольника», докажем теорему о средней линии треугольника и рассмотрим задачу на применение этой теоремы.

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

Теорема:

Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.

Докажем это утверждение.

Дано: ∆АВС, МN – средняя линия треугольника АВС.

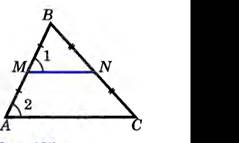
Доказать:

Доказательство:

Что и требовалось доказать.

Решим задачу, применяя теорему о средней линии треугольника.

Задача:

докажите, что медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.

Дано:

∆АВС, АA1, ВB1, СC1 – медианы треугольника.

Доказать:

АA1∩В B1∩СC1 = О

АО = 2A1О

ВО = 2B1О

СО = 2C1О

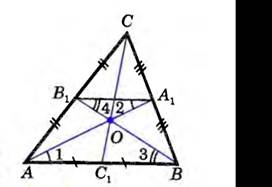
Доказательство:

проведем среднюю линию A1B1, по теореме о средней линии треугольника A1B1║АВ, поэтому ∠1 = ∠2 и ∠3 = ∠4 как накрест лежащие углы при пересечении параллельных прямых A1B1 и АВ секущими АA1 и ВB1.

Отсюда следует, что треугольники АОВ и A1OB1 подобны по первому признаку подобия треугольников, т.е. по двум равным углам, а значит, стороны этих треугольников пропорциональны:

Так как A1B1 – средняя линия треугольника АВС, то

АВ = 2A1B1, поэтому АО = 2A1O и ВО = 2B1O.

Таким образом, точка О – точка пересечения медиан АА1 и ВВ1 делит каждую из них в отношении 2:1, считая от вершин А и В.

Аналогично доказывается для медиан ВB1 и СC1, точка пересечения делит каждую из них в отношении 2:1, считая от вершин В и С, и, следовательно, эта точка совпадает с точкой О.

Таким образом, все три медианы пересекаются в одной точке О и делятся ею в отношении 2:1, считая от вершины.

Что и требовалось доказать.

Решенная задача имеет свое применение в других геометрических задачах и является одним из основных свойств для треугольника.