В этом уроке познакомимся с понятием «среднее геометрическое» или «среднее пропорциональное» для отрезков, выведем формулы для вычисления высоты и катетов прямоугольного треугольника через понятие среднее пропорциональное, рассмотрим задачу на применение формул.
Решим задачу:
Доказать, что высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.
Дано:
∆АВС – прямоугольный треугольник,
СD – высота, проведенная из вершины С к гипотенузе АВ.
Доказать:
∆АВС ~ ∆АСD;
∆АВС ~ ∆CBD
∆АСD ~ ∆CBD.
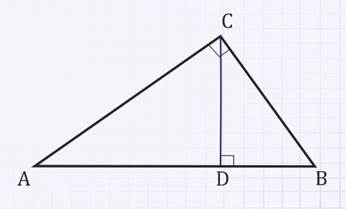
Доказательство:
1)Рассмотрим треугольники АВС и АСD.
Так как ∠А–общий,
∠АСВ = ∠АDС = 90°, отсюда следует, что треугольники АВС и АСD подобны по первому признаку подобия треугольников, т.е. по двум равным углам.
2)Рассмотрим треугольники АВС и СВD.
Так как ∠В–общий,
∠АСВ = ∠ВDС = 90°, то треугольники АВС и СВD тоже подобны по первому признаку подобия треугольников. А раз так, то ∠А = ∠ВСD.
3)Рассмотрим треугольники АСD и СВD.
Так как ∠АDС = ∠СDВ = 90° и ∠А = ∠ВСD, то треугольники АСD и СВD подобны по первому признаку подобия треугольников.
Что и требовалось доказать.
В геометрии в формулировках ряда утверждений и при решении отдельных задач используется понятие «среднее пропорциональное отрезков» или «среднее геометрическое».
Отрезок ХУ называется средним пропорциональным (или средним геометрическим) для отрезков АВ и СD, если выполняется равенство:
![]()
Исходя из доказанной выше задачи, можно выделить два утверждения.
1.Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой.
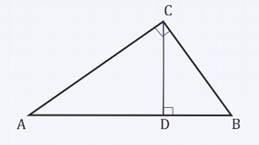
Для вывода данного утверждения воспользуемся доказанным, а именно, что:
![]()
поэтому:
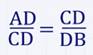
Применяя основное свойство пропорции, получим
![]()
2.Катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключенного между катетом и высотой, проведенной из вершины прямого угла.
Также по выше доказанному в задаче:
![]()
поэтому:
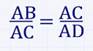
и, следовательно:
![]()
Решим задачу, применяя данные утверждения.
Задача:
Найдите катеты прямоугольного треугольника АВС, если АD = 24 см, ВD = 6 см.
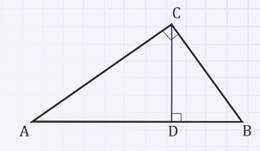
Решение:
Найдем гипотенузу данного прямоугольного треугольника:
![]()
Теперь воспользуемся равенством второго утверждения:
![]()
Для вычисления второго катета воспользуемся теоремой Пифагора:
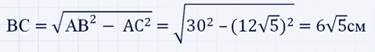
или равенством все того же второго утверждения:
![]()
 Подпишись и будь
в курсе новых событий и новостей!
Подпишись и будь
в курсе новых событий и новостей!