В этом уроке познакомимся с третьим признаком подобия треугольников и рассмотрим задачу на его применение.

Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.

Число, равное отношению сходственных сторон подобных треугольников, называют коэффициентом подобия.

Третьим признаком подобия треугольников является следующее утверждение:

Теорема:

Tсли три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.

Докажем это.

Доказательство:

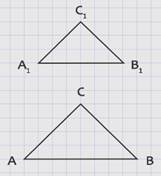
Учитывая второй признак подобия треугольников, а именно: «Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны», достаточно доказать, что ∠А = ∠А1.

Рассмотрим АВС2, у которого ∠1 = ∠А1 , ∠2 = ∠В1.

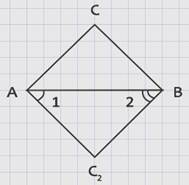
∆АВС2 и ∆А1В1С1 подобны по первому признаку подобия треугольников (так как два угла одного треугольника соответственно равны двум углам другого). Поэтому:

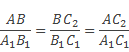
По условию теоремы:

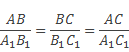
Из последних двух равенств стороны ВС и ВС2; АС и АС2 равны между собой.

Рассмотрим треугольники АВС и АВС2.

Они равны по трем сторонам (АВ – общая сторона, ВС = ВС2 , АС = АС2).

Из равенства треугольников АВС и АВС2 следует, что ∠А = ∠1, а так как ∠1 = ∠А1, то ∠А = ∠А1.

Что и требовалось доказать.

Решим задачу.

В прямоугольном треугольнике АВС катет АВ = 3 см, гипотенуза АС = 5 см.

Катеты МК и КР треугольника МКР равны √27 см и 4√3 см.

Подобны ли эти треугольники?

Решение:

Найдем в каждом из этих треугольников неизвестные стороны.

Оказалось, что стороны треугольника АВС пропорциональны сторонам треугольника МКР, значит, данные треугольники подобны по третьему признаку подобия.