§ 1  Прямоугольник и его свойства

На этом занятии мы дадим определение прямоугольнику и рассмотрим его свойства и признак.

Итак, определение:

Прямоугольником называется параллелограмм, у которого все углы прямые.

Так как прямоугольник является параллелограммом, то он обладает всеми свойствами параллелограмма:

1) в прямоугольнике противоположные стороны равны;

2) диагонали точкой пересечения делятся пополам.

Еще существует особое свойство прямоугольника, а именно:

Диагонали прямоугольника равны.

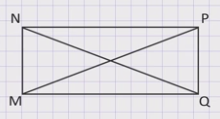
Докажем это утверждение. 

Дано:MNPQ - прямоугольник, МP и NQ – диагонали.

Доказать: МP= NQ. 

Доказательство: Рассмотрим ΔМPQ и ΔQNМ, они прямоугольные, у них сторона MQ является общей, и PQ=NM как противоположные стороны, значит, ΔМPQ = ΔQNМ по двум катетам. Отсюда следует, что гипотенузы МP и NQ этих треугольников равны. Что и требовалось доказать.