В этом уроке мы рассмотрим три признака параллелограмма и их применение при решении задач.

Первый признак:

если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм.

Докажем это утверждение.

Пусть в четырехугольнике АВСD стороны АВ и СD параллельны и АВ = СD. 

Докажем, что этот четырехугольник является параллелограммом.

Для этого проведем диагональ АС.

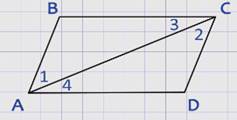
Рассмотрим два треугольника АВС и СDА.

Так как АС – общая сторона, АВ = СD по условию, ∠1 = ∠2 как накрест лежащие углы при параллельных прямых АВ и СD и секущей АС, следовательно, треугольники АВС и СDА равны по двум сторонам и углу между ними.

Если треугольники равны, то их соответствующие элементы равны, а значит ∠3 = ∠4.

А ∠3 и ∠4 являются накрест лежащими углами при пересечении прямых АD и ВС секущей АС, следовательно, АD параллельна ВС.

Итак, в данном четырехугольнике противоположные стороны попарно параллельны АВ параллельна СD и АD параллельна ВС, следовательно, по определению АВСD – параллелограмм, что и требовалось доказать.

Рассмотрим второй признак параллелограмма:

если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм.

Докажем и это утверждение.

Пусть в четырехугольнике АВСD АВ = СD и ВС = DА.

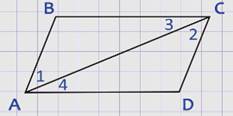
Для доказательства рассмотрим треугольники АВС и СDА.

Воспользуемся тем же построением. Так как АС – общая сторона, АВ = СD и ВС = DА по условию, то треугольники АВС и СDА равны по третьему признаку равенства треугольников, поэтому ∠1 = ∠2.

Отсюда следует, что АВ параллельна СD, поскольку ∠1 и ∠2 являются накрест лежащими углами при пересечении прямых АВ и СD секущей АС.

Так как АВ = СD и АВ параллельна СD, то по первому признаку параллелограмма четырехугольник АВСD – параллелограмм.

Третий признак параллелограмма:

если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.

Для доказательства данного утверждения рассмотрим четырехугольник АВСD, в котором диагонали АС и ВD точкой пересечения О делятся пополам.

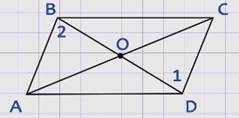
Треугольники АОВ и СОD равны по двум сторонам и углу между ними: АО = ОС, ВО = ОD по условию, ∠АОВ = ∠СОD как вертикальные углы, поэтому АВ = СD и ∠1= ∠2.

Из равенства этих углов следует, что АВ параллельна СD.

Таким образом, в четырехугольнике АВСD стороны АВ и СD равны и параллельны, значит, по первому признаку параллелограмма четырехугольник АВСD – параллелограмм.

А теперь решим задачу:

даны две окружности с общим центром О, в каждой из которых проведены диаметры КL и МN, не лежащие на одной прямой.

Нужно доказать, что четырехугольник МКNL – параллелограмм.

Выполним рисунок.

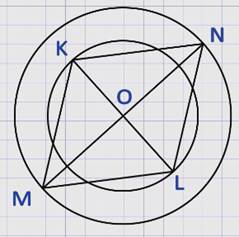
Нам дано:

две окружности с общим центром О, КL и МN – диаметры окружностей.

Необходимо доказать, что четырехугольник МКNL – параллелограмм.

Доказательство:

КО и ОL равны как радиусы первой, внутренней окружности;

ОМ и ОN равны как радиусы второй окружности, а КL и МN – диагонали четырехугольника МКNL.

Таким образом, диагонали четырехугольника точкой пересечения делятся пополам, а значит, по третьему признаку параллелограмма четырехугольник МКNL – параллелограмм.

Что и требовалось доказать.

Итак, в этом уроке Вы познакомились с признаками параллелограмма и рассмотрели решение задачи с использованием одного из них.