В этом уроке узнаем, какой четырехугольник называется параллелограммом, и рассмотрим свойства параллелограмма.

Параллелограммом называется выпуклый четырехугольник, у которого противоположные стороны попарно параллельны.

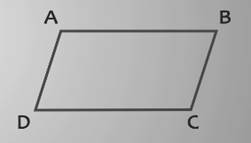
На рисунке представлен параллелограмм ABCD. У него сторона AB параллельна стороне CD, а сторона BC параллельна стороне AD.

Рассмотрим свойства параллелограмма.

Первое свойство:

в параллелограмме противоположные стороны равны и противоположные углы равны.

Докажем это свойство. 

Дано:

АВСD – параллелограмм.

Надо доказать, что стороны АВ и СD, АD и ВС, углы А и С, В и D равны.

Для доказательства:

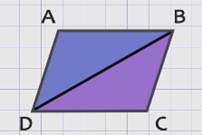
проведем диагональ ВD, которая делит параллелограмм на два треугольника: АВD и СDВ. В этих треугольниках ВD является общей стороной.

По определению параллелограмма противоположные стороны параллельны, а именно прямые АВ и СD параллельны, они пересечены секущей ВD, при этом углы АВD и ВDС являются накрест лежащими углами и для параллельных прямых АD и ВС, и секущей ВD; углы АDВ и DВС тоже накрест лежащие, а по признаку параллельности двух прямых накрест лежащие углы равны, значит, треугольники АВD и СDВ равны по стороне и двум прилежащим к ней углам, т.е. по второму признаку равенства треугольников.

Т.к. треугольники равны, то соответствующие стороны АВ и СD, АD и ВС равны и соответствующие углы А и С равны. А углы В и D равны сумме накрест лежащих равных углов, значит они тоже равны между собой. Что и требовалось доказать.

Рассмотрим второе свойство:

диагонали параллелограмма точкой пересечения делятся пополам.

Пусть точка О – есть точка пересечения диагоналей AD и BС параллелограмма ABDС.

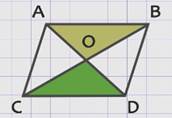
Треугольники AOB и COD равны между собой по стороне и двум прилежащим к ней углам, поскольку AB = CD как противоположные стороны параллелограмма; угол ВАО = углу СDО, угол АВО = углу DСО как накрест лежащие углы при параллельных прямых AB и CD и секущих СВ и АD соответственно.

Так как треугольники равны по второму признаку равенства треугольников, то все элементы треугольников AOB и COD будут равны, а значит AO = OD, OB = OС, что и требовалось доказать.

Рассмотрим задачу:

дан угол С параллелограмма АВСD, равный 48°.

Надо найти остальные углы.

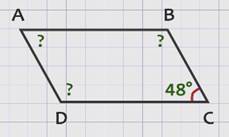
По свойству параллелограмма противоположные углы А и С равны, значит, угол А тоже равен 48°.

Сумма углов выпуклого четырехугольника равна 360°, а параллелограмм является выпуклым четырехугольником, поэтому для нахождения оставшихся противоположных углов В и D из 360° вычитаем сумму углов А и С и делим пополам, т.к. данные углы противоположные, и по свойству параллелограмма они тоже равны.

Вычисляя, получаем, что углы В и D равны по 132°.

Итак, в этом уроке Вы познакомились с понятием «параллелограмм» и рассмотрели свойства параллелограмма.