В этом уроке Вы узнаете, по каким правилам осуществляется умножение и деление алгебраических дробей, возведение их в степень, а также мы рассмотрим решение различных примеров на применение этих правил.

Умножение, деление и возведение алгебраических дробей в натуральную степень осуществляется по тем же правилам, что и для обыкновенных дробей.

А именно:

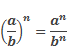
Чтобы умножить алгебраические дроби, необходимо умножить их числители (это будет числитель произведения) и умножить их знаменатели (это будет знаменатель произведения).

Деление на дробь – это умножение на перевёрнутую дробь, то есть, чтобы разделить две дроби, необходимо первую из них (делимое) умножить на перевёрнутую вторую (делитель).

А возведение алгебраической дроби в степень заключается в возведении в эту степень числителя и знаменателя по отдельности.

Прежде чем выполнять умножение, деление и возведение в натуральную степень алгебраических дробей, желательно их числители и знаменатели разложить на множители – это облегчит сокращение той алгебраической дроби, которая получится в результате.

Решим несколько примеров на применение этих правил:

Пример 1:

Выполнить умножение алгебраических дробей

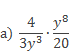
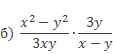
Решение:

a) По правилу умножения алгебраических дробей умножаем числитель первой дроби на числитель второй и аналогично для знаменателей данных дробей, при этом следует обратить внимание на знаменатель второй дроби – число 20 можно разложить на множители 4 и 5.

Далее следует числитель, и знаменатель полученной дроби разделить (сократить) на выражение 4y3 , получаем:

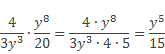
б) Для вычисления произведения дробей

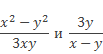
прежде следует разложить числитель первой дроби на множители:

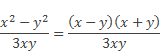
Затем перемножаем числители и перемножаем знаменатели дробей:

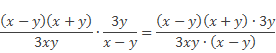
Полученное выражение можно сократить на

тогда будем иметь:

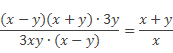
Пример 2:

Выполнить деление алгебраических дробей:

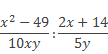
Решение:

Во-первых, разложим числители данных алгебраических дробей на множители:

получаем дроби

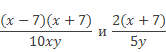
Во-вторых, выполним деление этих алгебраических дробей, для этого первую дробь умножим на перевёрнутую вторую, получаем:

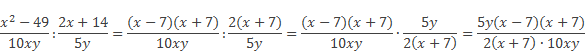
В-третьих, нужно сократить полученное алгебраическое выражение на

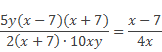
Таким образом, получили окончательный ответ.

А теперь давайте вспомним основные правила возведения целых выражений в натуральную степень:

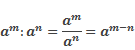
кроме этого, известно

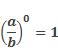
Используя эти правила, а также правило возведения алгебраических дробей в степень, решим следующий пример.

Пример 3:

Выполнить действия

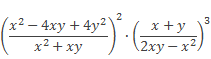
Решение:

Как и в предыдущих примерах разложим числители и знаменатели данных алгебраических дробей на множители:

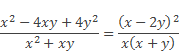
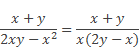
Затем возведем их в степень, используя рассмотренные выше правила:

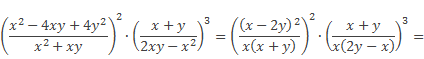
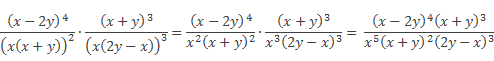
В знаменателе полученной дроби, чтобы из выражения

получить выражение

необходимое нам для последующего сокращения, следует вынести знак «–» за скобку, а затем поставить его перед дробью:

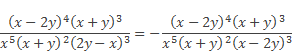
Далее сокращаем полученное алгебраическое выражение на

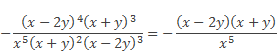
В заключение перенесем знак «–» в числитель полученной дроби

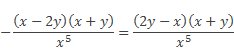
Итак, в этом уроке Вы повторили свойства степени и изучили правила умножения, деления и возведения в степень алгебраических дробей, кроме этого рассмотрели решение примеров различного уровня сложности.