В этом уроке рассмотрим алгоритм сложения и вычитания алгебраических дробей с разными знаменателями.
Давайте вспомним, как складывать и вычитать обыкновенные дроби с разными знаменателями.
Для этого необходимо привести дроби к общему знаменателю с помощью соответствующих дополнительных множителей, а затем сложить или вычесть полученные дроби с получившимися уже одинаковыми знаменателями.

Чтобы привести заданные дроби к знаменателю 12, определяем дополнительные множители для числителя и знаменателя каждой дроби: для первой это будет 3, а для второй –2.
Полученные дроби с одинаковыми знаменателями складываем, получаем:

Оказывается, что алгебраические дроби подчиняются тому же алгоритму.
Итак, алгоритм сложения (вычитания) алгебраических дробей с разными знаменателями:
1.Привести все дроби к общему знаменателю, если данные дроби имеют разные знаменатели.
2.Выполнить сложение (вычитание) полученных дробей с одинаковыми знаменателями.
Рассмотрим простой пример сложения алгебраических дробей с разными знаменателями.
Пример 1:
Выполнить действия

Решение:

![]()
Получаем:

Во-вторых, следует сложить полученные дроби с одинаковыми знаменателями, для этого составляем соответствующую алгебраическую сумму числителей, а знаменатель оставляем без изменений:
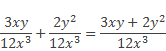
Нередко общим знаменателем дробей служит произведение выражений, стоящих в знаменателях данных дробей.
Рассмотрим такой случай.
Пример 2:
Выполнить действие:
![]()
Решение:

Таким образом, получаем
![]()
далее воспользуемся формулой разности квадратов в знаменателе, раскроем скобки и приведем подобные слагаемые в числителе полученной дроби:


![]()
Самое трудное в алгоритме сложения (вычитания) алгебраических дробей с разными знаменателями – это найти общий знаменатель.
В первом примере общим знаменателем алгебраических дробей

является произведение
![]()
которое состоит из наименьшего общего кратного числовых коэффициентов и повторяющегося в знаменателях обеих дробей буквенного множителя, причем взятого с большим показателем степени.
Во втором примере общим знаменателем дробей
![]()
является произведение
(![]()
которое состоит из знаменателей обеих данных дробей.
Итак, алгоритм приведения алгебраических дробей к общему знаменателю:
1.Разложить все знаменатели дробей на множители.
2.Найти наименьшее общее кратное для числовых коэффициентов, имеющихся в разложениях знаменателей на множители.
3.Выбрать все буквенные множители разложений знаменателей на множители, а повторяющиеся буквенные множители взять те, которые имеют больший показатель степени.
4.Составить произведение найденного из п.2 числового коэффициента и буквенных множителей из п.3. – это и будет общий знаменатель данных дробей.
5.Найти дополнительные множители для каждой из дробей: это будут произведения тех множителей, которые имеются в общем знаменателе, но которых нет в соответствующих знаменателях данных дробей.
6.Найти для каждой дроби новый числитель: это будет произведение старого числителя и дополнительного множителя.
7.Записать каждую дробь с новым числителем и общим знаменателем.
Применим оба алгоритма при решении следующего примера.
Пример 3:
Упростить выражение

Решение:
Во-первых, следует привести все 3 дроби к общему знаменателю. Для этого следует разложить все знаменатели на множители, а в знаменателе второй дроби вынести множитель (–1) за скобки, чтобы поменять знаки в знаменателе этой дроби на противоположные:

Общий знаменатель должен состоять из множителей, входящих во все знаменатели дробей, причем повторяющееся выражение
![]()
включаем с большим показателем степени.
Получим общий знаменатель:
![]()
Теперь найдем дополнительные множители для каждой дроби и умножим их на соответствующие числители и знаменатели, в итоге получим дроби с общим одинаковым для всех дробей знаменателем:
 =
=
Во-вторых, выполним сложение (вычитание) полученных дробей с одинаковыми знаменателями:
=![]()
Все выполненные преобразования действительны при допустимых значениях переменных а и b. В данном примере допустимыми являются все значения, кроме a = b, a = –b (в этих случаях знаменатели равны нулю).
Таким образом, в этом уроке Вы изучили алгоритм сложения (вычитания) алгебраических дробей с разными знаменателями, кроме этого применяли умения раскладывать многочлены на множители различными способами для нахождения общего знаменателя дробей.
 Подпишись и будь
в курсе новых событий и новостей!
Подпишись и будь
в курсе новых событий и новостей!