В этом уроке познакомимся с понятием «рациональное уравнение», разберем решение некоторых рациональных уравнений, а также рассмотрим пример математического моделирования задачи, которое приводит к возникновению соответствующего рационального уравнения.

В основе решения рациональных уравнений лежит техника преобразования рациональных выражений.

Рассмотрим пример 1 решения рационального уравнения:

Решение:

Известно, что дробь обращается в нуль при условиях, что числитель равен нулю, а знаменатель отличен от нуля.

Приравняв числитель полученной дроби к нулю, получаем:

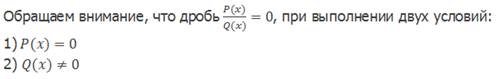
Выполнение второго условия обязательно следует проверять, т.к. возможно, что при выполнении первого условия, второе условие не выполняется.

Например, решим следующее уравнение примера 2:

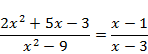
Решение:

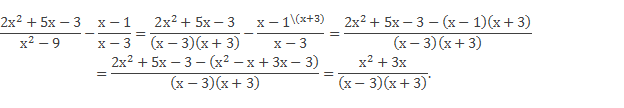
Получаем уравнение

Рассмотренные нами уравнения являются моделью для следующей текстовой задачи примера 3:

Катер прошел 12 км по течению реки и 4 км против течения реки, затратив на весь путь 2 ч.

Чему равна собственная скорость катера, если скорость течения реки равна 4 км/ч?

Решение:

Решение данной задачи осуществим с помощью метода математического моделирования и выделим 3 этапа данного метода.

Этап 1.

Тогда:

Этап 2.

Этап 3.

Ответ на вопрос задачи.

Итак, Вы рассмотрели примеры решения рациональных уравнений, а также их использование при решении текстовых задач.