В рамках этого урока рассмотрим правило сложения и вычитания алгебраических дробей с одинаковыми знаменателями, а также разберём решение нескольких типовых примеров с использованием этого правила.

Алгебраические дроби с одинаковыми знаменателями складывают и вычитают по тому же правилу, как и обыкновенные дроби, правило сводится к сложению и вычитанию их числителей, а знаменатель остается прежний.

Итак, следует запомнить следующие правило сложения и вычитания алгебраических дробей с одинаковыми знаменателями:

при сложении (вычитании) алгебраических дробей с одинаковыми знаменателями их числители складываются (вычитаются), а знаменатель остаётся прежний.

Другими словами, составляют соответствующую алгебраическую сумму числителей, а знаменатель оставляют без изменений.

Разберем несколько типовых примеров.

Пример 1:

Выполнить действия и упростить выражение:

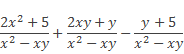
Решение:

Применим правило сложения и вычитания алгебраических дробей, составим соответствующую алгебраическую сумму числителей данных дробей, а знаменатель оставим без изменений. Из трех дробей мы получили одну, теперь в числителе этой дроби раскроем скобки и приведем подобные члены многочлена. При раскрытии скобок в числителе алгебраической дроби особое внимание следует уделить знаку «–» перед выражением

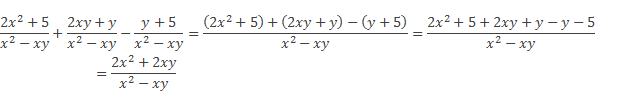
Мы получили дробь, которую необходимо упростить.

Для этого вынесем общий множитель за скобки в числителе и знаменателе дроби и сократим на переменную х:

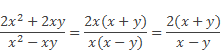
Таким образом, благодаря проделанным преобразованиям исходное выражение приобрело простой вид.

Важно отметить, что любое преобразование дробей имеет смысл только для тех значений переменной, которые принадлежат области ее определения.

Пример 2:

Выполнить действия с алгебраическими дробями:

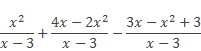
Решение:

Применяем правило сложения и вычитания алгебраических дробей с одинаковыми знаменателями, получаем дробь, числитель которой представляет алгебраическую сумму числителей данных дробей, а знаменатель тот же.

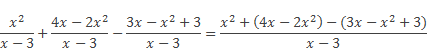
Далее следует раскрыть скобки в числители дроби, при этом особое внимание следует уделить знаку «–» перед второй скобкой:

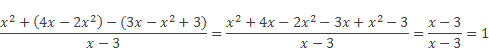
После приведения подобных членов многочлена в числителе мы получили выражение аналогичное выражению в знаменателе дроби.

Сокращаем эту дробь на выражение

в результате чего получается значение 1.

Известно, что знаменатель не может быть равен нулю, а значит,

Поэтому областью определения данного выражения являются все рациональные числа, кроме 3.

Итак, мы имели исходное выражение из трех алгебраических дробей, вычислили и получили, что при всех допустимых значениях х (т.е. все рациональные числа, кроме 3) выражение принимает значение 1.

Таким образом, в этом уроке Вы рассмотрели правило сложения и вычитания алгебраических дробей с одинаковыми знаменателями.