В этом уроке будем работать со степенями с отрицательными целыми показателями, а также докажем, что свойства степеней с натуральными показателями сохраняются и для отрицательных целых показателей.

Вспомним, что степенью неравного нулю числа aс натуральным показателем nназывается произведение n множителей, каждый из которых равен a:

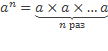
Вспомним также свойства степеней с натуральными показателями:

1)при умножении степеней с одинаковыми основаниями показатели складываются

2)при делении степеней с одинаковыми основаниями из показателя делимого надо вычесть показатель делителя

3)при возведении степени в степень показатели перемножаются

(аm)n = am – n

4)при возведении произведения в степень возводят в эту степень каждый из множителей

5)при возведении в степень дроби возводят в эту степень и числитель, и знаменатель дроби

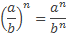
Важно при этом, что основания не равны нулю

В задачах на упрощение удобно пользоваться следующей записью этого определения.

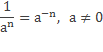
Решим несколько примеров на применение определения степени с отрицательным целым показателем.

Пример1:

Вычислить:

Решение:

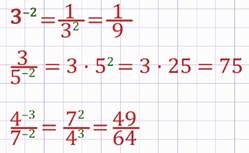
В третьем примере было применено важное тождество, которое часто используется на практике.

Любая дробь в отрицательной степени равна обратной дроби в этой степени:

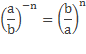
Вспомним также, что для любого ненулевого основания его нулевая степень должна равняться 1:

Пример 2.

Представить следующие числа в виде степеней числа 2:

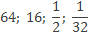
Решение:

Число 64 можно записать в виде произведения

Аналогично поступаем и с числом 16:

В следующем случае при решении используем формулу из определения степени с отрицательным целым показателем

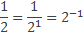
Для числа 1/32 в числителе дроби 1 представим как 20 и далее воспользуемся вторым свойством степени

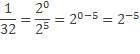
Рассмотрим несколько примеров с буквенными выражениями.

Пример 3:

Доказать, что

Решение:

а) Применим формулу из определения степени с отрицательным целым показателем а–2.

Т.е. получается, что при умножении степеней с одинаковыми основаниями показатели складываются

б) Вновь применим формулу из определения степени с отрицательным целым показателем

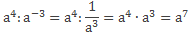
Т.е. получается, при делении степеней с одинаковыми основаниями из показателя делимого надо вычесть показатель делителя

в) Аналогично решим следующий пример

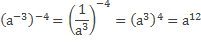
Получается, что при возведении степени в степень показатели перемножаются

Как Вы видите, привычные свойства степеней с натуральными показателями сохраняются и для отрицательных целых показателей.

Итак, в этом уроке Вы познакомились с понятием степени с отрицательным целым показателем, выяснили, что все свойства степеней с натуральными показателями остаются верными и для нового вида степеней. Также рассмотрели ряд примеров на применение этих свойств.