В этом уроке выясним, что в математике называется шаром и сферой, познакомимся с формулами объема шара и площади сферы.

Давайте представим себе футбольный мяч, теннисный шарик, горошину и апельсин.

Чем отличаются теннисный шарик и футбольный мяч от горошины и апельсина? Все они имеют форму шара, однако, теннисный шарик и мяч полые внутри. Для таких предметов в математике есть название – сфера. Горошина и апельсин, с точки зрения математиков, – это шары, а полые внутри теннисный шарик и футбольный мяч – это сферы.

Итак, дадим определения.

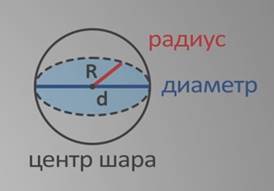
Шар — это геометрическое тело; совокупность всех точек пространства, находящихся от центра на расстоянии, не больше заданного.

Отрезок, соединяющий точку поверхности шара с его центром, называется радиусом шара.

Отрезок, соединяющий две точки поверхности шара и проходящий через центр шара, называют диаметром шара.

Поверхность шара называется сферой.

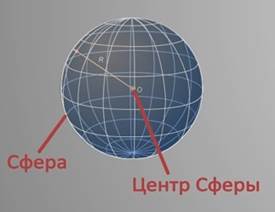
Сфера — это замкнутая поверхность, геометрическое место точек в пространстве, равноудалённых от данной точки, которую называют центром сферы.

Сферу невозможно развернуть на плоскости. Например, на географических картах земных полушарий полярные области изображены с искажением, они как бы растянуты.

С точки зрения математики шар – это пространственное тело, а значит, для него можно определить объем.

Сфера – поверхность шара, его оболочка, для нее определяется площадь. 

Формулы объема шара и площади сферы известны математикам уже давно.

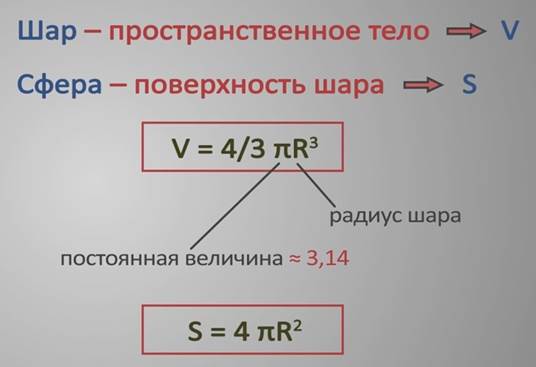
Объем шара вычисляется по формуле

где R – радиус шара, π – постоянная величина, обозначающая соотношение длины окружности и диаметра, приближенно равная 3,14.

Площадь сферы равна учетверенному произведению числа π и квадрата радиуса

В заключение немного истории.

Совершенство сферической формы издавна привлекало внимание мыслителей и учёных, которые с помощью сфер пытались объяснить гармонию окружающего мира. Например, у древних греков возникло представление о вращающейся хрустальной сфере, к которой прикреплены звёзды. Также в среде древнегреческих учёных появились космологические модели со сферической Землёй и прикреплёнными к вращающимся сферам из эфира планетами.

Итак, в этом уроке Вы узнали, что подразумевается под такими понятиями, как «шар» и «сфера», и познакомились с формулами объема шара и площади сферы.