В этом занятии сформулируем правила отыскания части от целого и целого по его части, а также рассмотрим решение задач с использованием этих правил.

Рассмотрим две задачи:

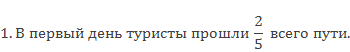
Сколько километров прошли туристы в первый день, если весь туристический маршрут 20 км.?

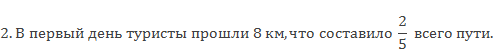
Найдите длину всего пути туристов.

Сравним эти задачи - в обеих за целое принят весь путь. В первой задаче целое известно – 20 км, а во второй – неизвестно. В первой задаче необходимо найти часть от целого, а во второй - целое по его части. Величина, известная в первой задаче 20 км, неизвестна во второй задаче, и наоборот, известное во второй задаче – 8 км, в первой необходимо найти. Такие задачи называются взаимно обратными, так как в них известные и искомые величины меняются местами.

Рассмотрим первую задачу:

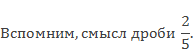
Знаменатель 5 показывает, на сколько частей разделили целое, т.е. если целое 20 разделить на 5, узнаем, сколько километров составляет одна часть, 20: 5 = 4 км. Числитель 2 показывает, что туристы прошли 2 части пути, значит 4 надо умножить на 2, получится 8 км. В первый день туристы прошли 8 км.

Получилось выражение 20 : 5 ∙ 2 = 8.

Перейдем ко второй задаче.

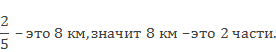
Следовательно, одна часть будет равна частному 8 и 2, получится 4, знаменатель 5, значит, всего частей 5.

4 умножить на 5, получится 20. Ответ 20 км длина всего пути.

Запишем выражение: 8 : 2 ∙ 5 = 20

Используя смысл умножения и деления числа на дробь, правила отыскания части от целого и целого по его части можно сформулировать так:

Чтобы найти часть от целого, надо число, соответствующее целому, умножить на дробь, соответствующую этой части;

чтобы найти целое по его части, надо число, соответствующее этой части, разделить на соответствующую части дробь.

Соответственно решение задач можно записать теперь по другому:

для первой задачи 20 ∙ 2/5 = 8 (км),

для второй задачи 8 : 2/5 = 20 (км).

Чтобы не было затруднений, решение подобных задач записываем так:

Целое: весь путь, известно – 20 км.

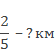
Ответ: 8 км.

Целое: весь путь – неизвестно.

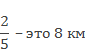
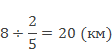
Ответ: 20 км.

Составим алгоритм решения подобных задач.

Сначала проанализируем условие и вопрос задачи: выясним, что является целым, известно оно или нет, далее выясним, как представлена часть целого и что нужно найти.

Если необходимо найти часть от целого, то целое умножим на дробь, соответствующую этой части, если надо найти целое по его части, то число, соответствующее части разделим на дробь, соответствующую этой части. В результате получим выражение. Далее найдем значение выражения и запишем ответ, прочитав перед этим еще раз вопрос задачи. 

Итак, прежде чем решать подобные задачи, необходимо ответить на следующие вопросы:

Какая величина прията за целое?

Известна ли эта величина?

Что требуется найти: часть от целого или целое по его части?

Подведем итоги: в этом уроке Вы познакомились с правилами отыскания части от целого и целого по его части, а также научились решать задачи по этим правилам.