Познакомимся с теоремой Виета, с соотношениями между корнями квадратного уравнения и его коэффициентами, научимся раскладывать квадратный трёхчлен на множители.

Квадратным уравнением называют уравнение вида ax2 + bx + c = 0, где a, b, c-коэффициенты, х – переменная, причём a ≠ 0. Левая часть квадратного уравнения

ax2 + bx +c – это многочлен второй степени, его называют квадратным трехчленом. Если в квадратном уравнении коэффициент при х2 или, можно сказать, старший коэффициент a равен 1, то такое квадратное уравнение называют приведенным.

Впервые зависимость в виде соотношений между корнями квадратного уравнения и его коэффициентами обнаружил французский математик Франсуа Виет.

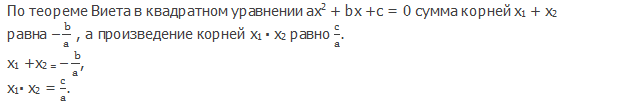
Докажем теорему Виета.

Теорема Виета справедлива и для квадратных уравнений, имеющих один корень. В этом случае считают, что уравнение имеет два одинаковых корня.

Теорему Виета удобно применять для приведенного квадратного уравнения:

Приведенное квадратное уравнение можно записать в виде:

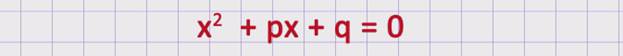
Тогда сумма корней х1 +х2 равна второму коэффициенту, взятому с противоположным знаком, то есть – р, а произведение корней х1∙ х2 равно свободному члену q.

х1 +х2 = – р

х1∙ х2 = q

По теореме Виета можно подбором найти корни уравнения. 

Например, решим квадратное уравнение х2 – х – 12 = 0. 

Уравнение является приведенным, так как коэффициент a равен 1. Тогда сумма корней х1 + х2 = 1, а произведение х1 ∙ х2= –12. Если х1 и х2 целые числа, то они являются делителями числа –12. Нетрудно догадаться, что х1 = –3; х2 = 4.

По теореме обратной теореме Виета можно выполнить проверку правильности нахождения корней квадратного уравнения. 

Обратное утверждение теоремы Виета:

Если х1 и х2 – корни квадратного уравнениятакие, чтох1 + х2 = –р, х1 ∙ х2 = q, то эти числа0 – корни уравнения х2 + рх + q = 0.

Решим уравнение 3х2 – 4х – 4 = 0.

Дискриминант D= (-4)2 -4 ∙ 3 ∙ (-4) = 64, D > 0.

Найдем корни:

С помощью теоремы Виета выводится формула разложения квадратного трехчлена на множители.

В квадратном трехчлене ax2 + bx +c вынесем за скобки a. Получим:

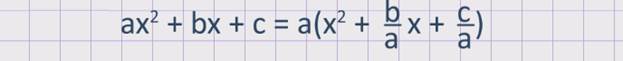
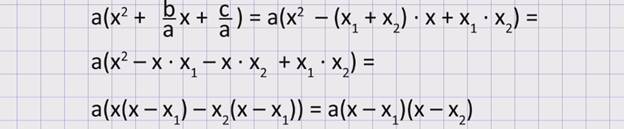
Значит, квадратный трехчленможно разложить на множители ax2 + bx + c = a(х– х1) (х –х2),где х1 и х2 – корни квадратного трехчлена, которые можно найти, решая квадратное уравнение ax2 + bx + c = 0.

Если х1 = х2 , т.е. дискриминант квадратного трехчлена равен нулю (D = 0), то доказанная формула будет иметь вид ax2 + bx + c = a(х– х1)2.

Разложим на множители квадратный трехчлен 3х2 – 10х + 3. 

Для этого решим квадратное уравнение 3х2 – 10х + 3 = 0.

Дискриминант D = = (-10)2 – 4 ∙ 3 ∙ 3 = 64, D > 0.

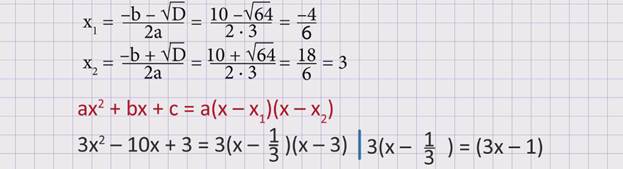
Тогда 3х2 – 10х + 3 = (3х – 1)(х – 3).

Тогда сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком х1 +х2 = –р, а произведение корней равно свободному члену х1∙ х2 = q. Эти соотношения впервые обнаружил французский математик Франсуа Виет.

По теореме Виета можно подбором найти корни уравнения.

Если свободный член q – отрицательное число, то корни имеют разные знаки. По теореме, обратной теореме Виета, можно проверить правильность нахождения корней.

С помощью теоремы Виета выводится формула разложения квадратного трёхчлена на множители a x2 + bx +c= a(х - х1) (х -х2), где х1; х2 – корни квадратного трехчлена.