В этом уроке разберем такие понятия, как рациональное уравнение, рациональное выражение, целое выражение, дробное выражение. Рассмотрим решение рациональных уравнений.

Рациональным уравнением называют уравнение, в котором левая и правая части являются рациональными выражениями.

Рациональные выражения бывают:

– целые;

– дробные.

Целое выражение составлено из чисел, переменных, целых степеней с помощью действий сложения, вычитания, умножения, а также деления на число, отличное от нуля.

Например:

В дробных выражениях есть деление на переменную или выражение с переменной. Например:

Дробное выражение не при всех значениях входящих в него переменных имеет смысл. Например, выражение

при х = –9 не имеет смысла, так как при х = –9 знаменатель обращается в нуль.

Значит, рациональное уравнение может быть целым и дробным.

Целое рациональное уравнение – это рациональное уравнение, в котором левая и правая части – целые выражения.

Например:

Дробное рациональное уравнение – это рациональное уравнение, в котором или левая, или правая части – дробные выражения.

Например:

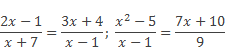
Рассмотрим решение целого рационального уравнения. 

Например:

Умножим обе части уравнения на наименьший общий знаменатель знаменателей входящих в него дробей.

Для этого:

1. найдем общий знаменатель для знаменателей 2, 3, 6. Он равен 6; 

2. найдем дополнительный множитель для каждой дроби. Для этого общий знаменатель 6 делим на каждый знаменатель

дополнительный множитель для дроби

равен 3,

дополнительный множитель для дроби

равен 2,

дополнительный множитель для дроби

равен 1; 

3. умножим числители дробей на соответствующие им дополнительные множители. Таким образом, получим уравнение

которое равносильно данному уравнению

Слева раскроем скобки, правую часть перенесем налево, изменив знак слагаемого при переносе на противоположный.

Приведем подобные члены многочлена и получим

Видим, что уравнение линейное.

Решив его, найдем, что х = 0,5.

Рассмотрим решение дробного рационального уравнения. 

Например:

1.Умножим обе части уравнения на наименьший общий знаменатель знаменателей входящих в него рациональных дробей.

Найдем общий знаменатель для знаменателей х + 7 и х – 1.

Он равен их произведению (х + 7)(х – 1).

2.Найдем дополнительный множитель для каждой рациональной дроби.

Для этого общий знаменатель (х + 7)(х – 1) делим на каждый знаменатель. Дополнительный множитель для дроби

равен х – 1,

дополнительный множитель для дроби

равен х+7.

3.Умножим числители дробей на соответствующие им дополнительные множители.

Получим уравнение (2х – 1)(х – 1) = (3х + 4)(х + 7), которое равносильно данному уравнению

4.Слева и справа умножим двучлен на двучлен и получим следующее уравнение

5.Правую часть перенесем налево, изменив знак каждого слагаемого при переносе на противоположный:

6.Приведем подобные члены многочлена:

7.Можно обе части разделить на –1. Получим квадратное уравнение:

8.Решив его, найдем корни

Так как в уравнении

левая и правая части – дробные выражения, а в дробных выражениях при некоторых значениях переменных знаменатель может обратиться в нуль, то необходимо проверить, не обращается ли в нуль при найденных х1 и х2 общий знаменатель.

При х = –27 общий знаменатель (х + 7)(х – 1) не обращается в нуль, при х = –1 общий знаменатель также не равен нулю.

Следовательно, оба корня –27 и –1 являются корнями уравнения.

При решении дробного рационального уравнения лучше сразу указать область допустимых значений. Исключить те значения, при которых общий знаменатель обращается в нуль.

Рассмотрим еще один пример решения дробного рационального уравнения. 

Например, решим уравнение

Знаменатель дроби правой части уравнения разложим на множители

Получим уравнение

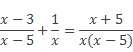
Найдем общий знаменатель для знаменателей (х – 5), х, х(х – 5).

Им будет выражение х(х – 5).

теперь найдем область допустимых значений уравнения

Для этого общий знаменатель приравняем к нулю х(х – 5) = 0.

Получим уравнение, решив которое, найдем, что при х = 0 или при х = 5 общий знаменатель обращается в нуль.

Значит, х = 0 или х = 5 не могут быть корнями нашего уравнения.

Теперь можно найти дополнительные множители.

Дополнительным множителем для рациональной дроби

будет х,

дополнительным множителем для дроби

будет (х – 5),

а дополнительный множитель дроби

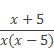
равен 1.

Числители умножим на соответствующие дополнительные множители.

Получим уравнение х(х – 3) + 1(х – 5) = 1(х + 5).

Раскроем скобки слева и справа, х2 – 3х + х – 5 = х + 5.

Перенесем слагаемые справа налево, изменив знак переносимых слагаемых:

Х2 – 3х + х – 5 – х – 5 = 0

И после приведения подобных членов получим квадратное уравнение х2 – 3х – 10 = 0. Решив его, найдем корни х1 = –2; х2 = 5.

Но мы уже выяснили, что при х = 5 общий знаменатель х(х – 5) обращается в нуль. Следовательно, корнем нашего уравнения

будет х = –2.

Важно запомнить:

При решении дробных рациональных уравнений надо поступить следующим образом:

1.Найти общий знаменатель дробей входящих в уравнение. При этом если знаменатели дробей можно разложить на множители, то разложить их на множители и затем найти общий знаменатель.

2.Умножить обе части уравнения на общий знаменатель: найти дополнительные множители, умножить числители на дополнительные множители.

3.Решить получившееся целое уравнение.

4.Исключить из его корней те, которые обращают в нуль общий знаменатель.