Разберем решение текстовых задач с помощью составления рациональных уравнений, которые будут выступать в качестве математических моделей этих задач.
Рациональным уравнениемназывают уравнение, в котором левая и правая части являются рациональными выражениями. Рациональные выражения бывают целые и дробные. Соответственно, рациональное уравнение может быть как целым, так и дробным. В целых рациональных уравнениях левая и правая части являются целыми выражениями.
Например, уравнение:
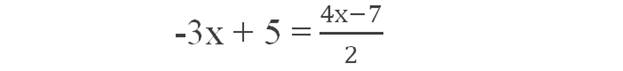
является целым рациональным уравнением. В дробных рациональных уравнениях или левая, или правая, или обе части уравнения являются дробными выражениями. Например, уравнения:
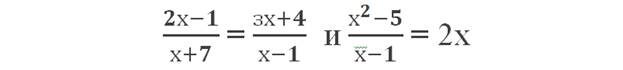
являются дробными.
Поэтому при решении текстовых задач математической моделью может быть как целое, так и дробное рациональное уравнение. Это зависит от условия конкретной задачи.
ЗАДАЧА 1.
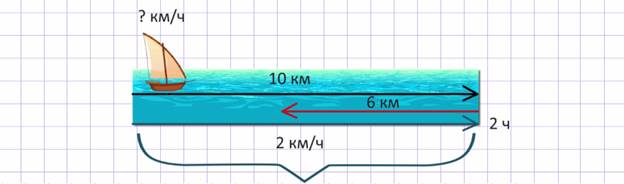
Лодка прошла 10 км по течению реки и 6 км против течения, затратив на весь путь 2 ч. Чему равна собственная скорость лодки, если скорость течения реки равна 2 км/ч?
Первый этап. Составление математической модели.
Пусть х км/ч – собственная скорость лодки. Лодка плыла как по течению, так и против течения, скорость лодки по течению будет равна (х+2) км/ч, а скорость против течения равна (х-2) км/ч. По течению лодка прошла 10 км. Найдем время, затраченное на путь
по течению. Чтобы найти время, надо расстояние разделить на скорость. Время, затраченное на путь по течению, будет равно 10/x + 2 ч. Против течения лодка прошла 6 км. Значит, время, затраченное на путь против течения, 6/ x – 2 ч. По условию задачи на весь путь лодка затратила 2 ч. Следовательно, имеем уравнение:
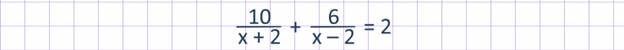
Оно является математической моделью данной задачи.
Второй этап. Работа с составленной моделью.


Оба значения не обращают в нуль общий знаменатель (х+2)(х-2), следовательно, эти значения – корни нашего дробного рационального уравнения.
Третий этап. Ответ на вопрос задачи.
За х в задаче принята собственная скорость лодки. Но собственная скорость лодки не может быть равна 0 км/ч. Поэтому в качестве ответа на вопрос задачи надо взять один из полученных корней уравнения, а именно х = 8. Ответ: собственная скорость лодки равна 8 км/ч.
ЗАДАЧА 2.
Сумма катетов прямоугольного треугольника равна 23 см. Найдите катеты треугольника, если его гипотенуза равна 17см.
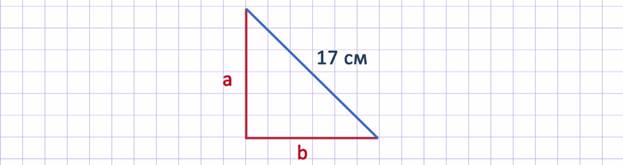
Первый этап. Составление математической модели.
Пусть х см один из катетов треугольника, тогда другой катет равен (23-х) см. Так как треугольник прямоугольный, то для составления уравнения воспользуемся теоремой Пифагора: «В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов». Получим уравнение х2 + (23-х)2 = 172 . Это уравнение является математической моделью нашей задачи.
Второй этап. Работа с составленной моделью.
Уравнение х2 +(23-х)2 =172 является целым рациональным уравнением. Раскроем скобки в левой его части, перенесем 172 справа налево, изменив при этом знак, получим уравнение х2 + 529-46х+х2 – 289 = 0. Приведем подобные члены. Имеем квадратное уравнение:
2х2 – 46х + 240 = 0
Решая его, найдем, что х1 = 8, х2 = 15.
Третий этап. Ответ на вопрос задачи.
За х в задаче принят один из катетов. Найдем другой катет. Так как другой катет равен (23 – х) см, то, подставляя в это выражение найденные корни уравнения, вместо х будем иметь: 23 – 8 = 15 см и 23 – 15 = 8 см. Любая пара 8 см и 15 см или 15 см и 8 см удовлетворяет условию задачи.
Ответ: Катеты прямоугольного треугольника равны 8 см и 15 см.
ЗАДАЧА 3.
Один кран наполняет бассейн на 6 ч быстрее другого. Два крана, работая вместе, наполняют бассейн за 4 ч. За сколько часов может наполнить водой бассейн каждый кран, работая отдельно?

Рациональные уравнения могут выступать в качестве математических моделей при решении текстовых задач.
Решая такие задачи, надо учитывать особенности каждого этапа их решения.
Первый этап – составление математической модели. Математической моделью может быть как целое, так и дробное рациональное уравнение.
Второй этап – работа с составленной моделью. Решаем рациональное уравнение.
Третий этап – ответ на вопрос задачи. Проверяем, подходят ли найденные корни рационального уравнения условию задачи.
 Подпишись и будь
в курсе новых событий и новостей!
Подпишись и будь
в курсе новых событий и новостей!