В этом уроке выведем формулы для решения квадратных уравнений с чётным вторым коэффициентом и научимся решать такие квадратные уравнения, используя эти формулы.

Квадратным уравнением называют уравнение вида ax2 + bx +c=0, где a называют первым или старшим коэффициентом, b – вторым коэффициентом или коэффициентом при х, с – свободным членом, х – переменная, причём a ≠ 0.

Чтобы решить квадратное уравнение, необходимо найти дискриминант D по формуле

D = b2 – 4ac

Если в квадратном уравнении коэффициент b- четное число, то это уравнение можно представить в виде ax2 + 2kx + c=0, где b=2k, k – целое число.

Выведем формулы для решения квадратного уравнения с четным вторым коэффициентом. Для этого в основную формулу для решения квадратного уравнения вместо второго коэффициента b подставим 2k.

Найдем дискриминант.

D = b2 – 4ac = (2k)2 – 4ac = 4k2 – 4ac.

Вынесем за скобки 4 и получим D = 4(k2 – ac).

Обозначим выражение в скобках за D1. Тогда D1 = k2 – ac, а D = 4D1.

Видно, что число корней уравнения зависит от D1. Если D1 больше нуля, то уравнение имеет два корня.

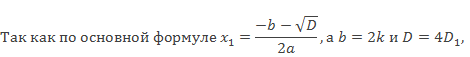
Разделим числитель и знаменатель на 2. После всех преобразований формула примет вид

Корни х1 и х2 зависят только от знака квадратного корня в числителе, поэтому

А если дискриминант D1 равен нулю? Уравнение будет иметь один корень.

Вместо коэффициента b подставим 2k.

Рассмотрим решение квадратного уравнения 5х2 –16 х + 3 = 0 как по основной формуле, так и по формуле с четным вторым коэффициентом. А затем сделаем некоторые выводы. 

Итак, сначала выпишем коэффициенты a = 5, b= –16, с = 3.

Найдем дискриминант D по формуле D = b2 – 4ac.

Подставив в неё значения коэффициентов, получим D= (–16)2 – 4 ∙ 5 ∙ 3 = 196,дискриминант больше нуля D>0, значит, уравнение имеет два корня, используя соответствующие формулы, вычисляем:

Так как коэффициент b= –16 четное число, то можно решить это уравнение по формулам решения квадратного уравнения с четным вторым коэффициентом. 

В нашем уравнении 5х2 –16х + 3 = 0, k = –16:2= –8.

Найдем дискриминант D1.

D1 = k2 –ac= (–8)2 – 5 ∙ 3 = 49, он больше нуля D1 >0, уравнение имеет два корня, которые находим по соответствующим формулам:

Заметим, что корни получились одинаковые х1 = 0,2; х2 = 3.

Однако есть преимущества в использовании формул решения квадратного уравнения с четным вторым коэффициентом.

Во-первых, при нахождении дискриминанта в квадрат возводится не число b, не второй коэффициент, а его половина и вычитается из этого квадрата не 4ac, а просто ac

Во-вторых, при нахождении корней в знаменателе не 2a, а просто a.

В-третьих, дискриминант, находимый по формуле с четным вторым коэффициентом, то есть D1, в 4 раза меньше дискриминанта D.

Если квадратное уравнение с четным вторым коэффициентом b=2k и с коэффициентом a= 1, т.е. является приведенным x2 + 2kx +c=0, то решить уравнение можно ещё проще. Находим дискриминант по формуле D1 = k2 – c.

Если он больше нуля D1 >0, то корни находим по формулам:

Если дискриминант равен нулю D1=0, то будет один корень х = –k.

Рассмотрим решение квадратного уравнения х2 +10 х–5600 = 0 как по основной формуле, так и по формуле решения квадратного уравнения с четным вторым коэффициентом, являющееся приведенным.

Выпишем коэффициенты a = 1, b= 10, с = – 5600.

Найдем дискриминант D по формуле D = b2 – 4ac.

D = (10)2 – 4 ∙ 1 ∙ (–5600) = 22500, D > 0, дискриминант положительный, значит, уравнение имеет два корня, используя соответствующие формулы, получим значения корней:

Так как коэффициент b = 10 четное число, то можно решить это уравнение по формуле решения квадратного уравнения с четным вторым коэффициентом. Заметим, что в уравнении коэффициент a=1.

Уравнение является приведенным.

k = 10 : 2 = 5.

Найдем дискриминант D1.

Важно запомнить:

Если квадратное уравнение ax2 + bx + c = 0 с четным вторым коэффициентом, то есть второй коэффициент можно представить в виде b = 2k, k – целое число, то уравнение лучше решить по соответствующим формулам. При решении поступают следующим образом:

1.Находят дискриминант D1 по формуле D1 = k2 – ac. Значение дискриминанта зависит от коэффициентов a, k , с.

2.Сравнивают дискриминант D1 с нулём.

3.Если дискриминант больше нуля, то уравнение ax2 + 2kx +c=0 имеет два корня

Если дискриминант меньше нуля, корней нет.

4.Если квадратное уравнение ax2 + bx + c = 0 с четным вторым коэффициентом и является приведенным x2 + 2kx + c = 0, коэффициенты a= 1, b = 2k, k – целое число, то уравнение решают следующим образом:

1)Находят дискриминант D1 по формуле D1 = k2 – c.

2)Сравнивают дискриминант D1 с нулём.

3)Если дискриминант больше нуля, то уравнение x2 + 2kx +c=0 имеет два корня

Если дискриминант равен нулю, то х = –k.

Если дискриминант меньше нуля, корней нет.