В этом уроке разберем такие понятия, как квадратное уравнение, квадратный трехчлен, дадим определение неполного квадратного уравнения, определение приведенного квадратного уравнения и рассмотрим решение наиболее простых уравнений – неполных квадратных уравнений.

Квадратным уравнением называют уравнение вида ax2 + bx + c = 0, где a, b, c –некоторые числа, х – переменная, причём a ≠ 0.

Числа a, b, c называют коэффициентами квадратного уравнения.

Причем, a называют первым или старшим коэффициентом, b – вторым коэффициентом или коэффициентом при х, c – свободным членом.

Например, квадратное уравнение 2х2 – 4х – 7 = 0 имеет коэффициенты

старший: a = 2,

коэффициент при х: b = –4,

свободный член: с = –7.

Левая часть квадратного уравнения ax2 + bx + c – это многочлен второй степени.

Поэтому квадратное уравнение называют уравнением второй степени. А многочлен

ax2 + bx + c называют квадратным трехчленом.

Если в квадратном уравнении старший коэффициент a равен 1или, можно сказать, коэффициент при х2 равен 1, то такое квадратное уравнение называют приведенным. Например, уравнение 2х2 – 4х – 7 = 0 не является приведенным, так как коэффициент a равен 2. А уравнение х2 + 4х – 1 = 0 – приведенное квадратное уравнение.

Любое квадратное уравнение можно сделать приведенным. Для этого надо обе части уравнения разделить на коэффициент a.

Например, в уравнении 2х2 – 4х – 7=0 разделим обе части уравнения на 2.

Получим равносильное данному приведенное квадратное уравнение х2 – 2х – 3,5=0.

Рассмотрим вопрос о корнях квадратного уравнения. Так как левая часть квадратного уравнения – это многочлен второй степени, то уравнение может иметь два корня. Корнем квадратного уравнения ax2 + bx +c=0 называют значение переменной х, при котором квадратный трехчлен равен нулю. Вообще, решить уравнение - значит найти все его корни или установить, что корней нет.

Любое квадратное уравнение, приведенное или неприведенное, является полным квадратным уравнением. В полном квадратном уравнении все три коэффициента отличны от нуля.

Т.е. присутствуют все три слагаемых – ax2, bx и c.

Кроме полных квадратных уравнений есть неполные квадратные уравнения.

Неполное квадратное уравнение – это уравнение, в котором хотя бы один из коэффициентов b или с равен нулю. В таком уравнении присутствуют не все три слагаемых. Но стоит обратить внимание, что по определению квадратного уравнения, слагаемое ax2 всегда присутствует в квадратном уравнении.

Рассмотрим виды неполных квадратных уравнений. Их три. Научимся решать.

Первый вид.

Если коэффициент b = 0, то квадратное уравнение принимает вид ax2 + c = 0.

Решим его. 

1) Перенесем свободный член слева направо, не забудем, при переносе слагаемого меняем его знак. Получим: ax2 = –c.

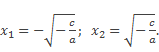
Например, решим уравнение –3 x2 + 21 = 0.

Перенесем свободный член в правую часть уравнения.

Получим –3 x2 = –21.

Разделим обе части на –3.

Получаем х2=7.

7>0.

Значит, уравнение имеет два корня.

Рассмотрим еще одно уравнение.

2х2 + 8 = 0.

Перенесем 8 слева направо.

Получим 2х2 = –8.

Разделим обе части на 2.

Уравнение примет вид х2 = –4.

Так как –4 < 0, то такое уравнение корней не имеет.

Рассмотрим второй вид неполных квадратных уравнений.

Если коэффициент с = 0, то квадратное уравнение принимает вид ax2 + bx = 0. 

Решим его. 

1) Разложим на множители левую часть уравнения, вынесением за скобку х. 

Получим х(ax + b) = 0. 

2) Рассуждаем, в каком случае произведение равно нулю.

Если первый множитель х = 0 или второй множитель aх + b=0.

Решаем уравнение aх + b = 0.

aх = –b

Значит, уравнение ax2 + bx = 0 имеет два корня

Надо заметить, что неполное квадратное уравнение вида ax2 + bx = 0 при b ≠ 0 всегда имеет два корня.

Например, решим уравнение 4x2 – 7x = 0.

Вынесем за скобки х.

Получаем х(4х – 7) = 0.

Отсюда х1 = 0.

Решая уравнение 4х – 7 = 0, находим второй корень х2 = 1,75.

Третий вид неполных квадратных уравнений.

Если коэффициент b = 0 и коэффициент с = 0, то квадратное уравнение принимает вид

ax2 = 0.

Такое квадратное уравнение равносильно уравнению x2 = 0. Поэтому имеет единственный корень х = 0.

Неполное квадратное уравнение в зависимости от его вида может иметь два корня, один корень и не иметь корней.

Важно запомнить:

Квадратным уравнением называют уравнение вида ax2 + bx + c = 0, где a, b, c – коэффициенты, х – переменная, причём a ≠ 0.

Многочлен ax2 + bx + c называют квадратным трёхчленом.

Квадратное уравнение ax2 + bx + c = 0 называют приведенным, если коэффициент a = 1.

Полное квадратное уравнение, это уравнение в котором присутствуют все три слагаемых или все коэффициенты a, b, с, отличны от нуля.

Неполным квадратное уравнение называют, если b = 0 или с = 0, или b = 0 и с = 0.

Если уравнение имеет вид ax2 = 0, то оно имеет один корень х = 0.

Если уравнение имеет вид ax2 + bx = 0, для его решения раскладываем левую часть на множители х(ax + b) = 0.

Если уравнение имеет вид ax2 + c = 0, решаем его переносом свободного члена слева направо. Далее обе части делим на коэффициент a.

Если правая часть равенства больше нуля, то уравнение имеет два корня

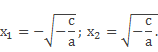
Иначе, корней нет.