Познакомимся со свойствами квадратных корней, чтобы в дальнейшем использовать их при извлечении квадратных корней из неотрицательных чисел.

Докажем это утверждение.

Доказательство:

Воспользуемся определением квадратного корня: квадратным корнем из неотрицательного числаaназывается такое неотрицательное число b, квадрат которого равен a:

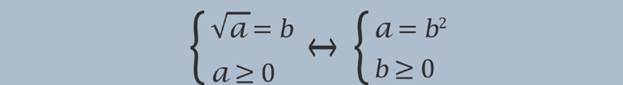
То есть:

а с другой стороны:

Получаем, что:

Если квадраты двух неотрицательных чисел равны, то и сами числа равны, значит, из равенства квадратов, получаем равенство:

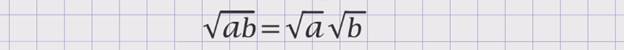
Таким образом, свойство доказано.

Данное свойство справедливо и для большего числа неотрицательных множителей: