В этом уроке узнаем, что подразумевается под понятием «множество действительных чисел», а также рассмотрим основные свойства действительных чисел.
Множество рациональных чисел обозначается заглавной английской буквой Q. Оно включает в себя множество целых чисел (Z) и множество натуральных чисел (N). Если множество рациональных чисел Q дополнить множеством иррациональных чисел (I), то вместе они составят множество действительных чисел, которое обозначают буквой R или символической записью (-∞;+∞).
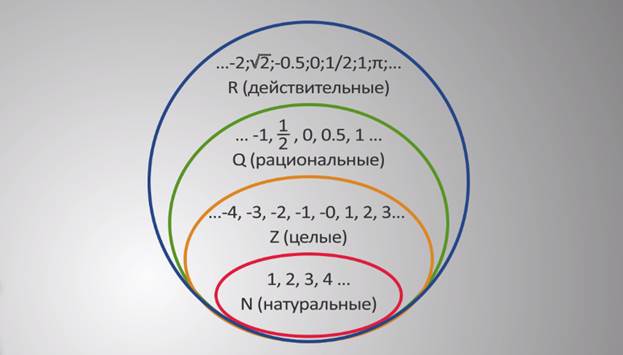
Множество действительных чисел – это множество конечных и бесконечных десятичных дробей; конечные десятичные дроби и бесконечные десятичные периодические дроби – рациональные числа, а бесконечные десятичные непериодические дроби – иррациональные числа.
Итак, мы выяснили, что же такое множество действительных чисел и из чего оно состоит (из множеств рациональных и иррациональных чисел).
Каждое действительное число можно изобразить точкой на координатной прямой. Так же верно, что каждая точка координатной прямой имеет действительную координату.
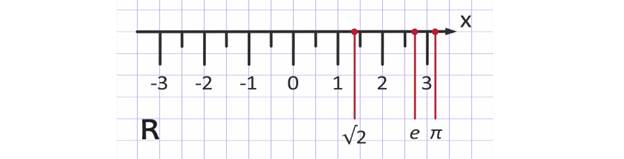
Таким образом, существует взаимооднозначное соответствие между множеством точек координатной прямой и множеством действительных чисел, т. е. каждому действительному числу соответствует единственная точка на координатной прямой, и наоборот, каждой точке координатной прямой соответствует единственное действительное число. Координатная прямая является геометрической моделью множества действительных чисел, еще её называют числовой прямой.
Основные формулы и законы, которые очень полезны при преобразованиях или упрощениях громоздких и простых выражений, например, формула разности квадратов, правило перемещения при сумме и произведении, ассоциативное правило и др., выполняются не только для рациональных, но и для любых допустимых действительных значений переменных:
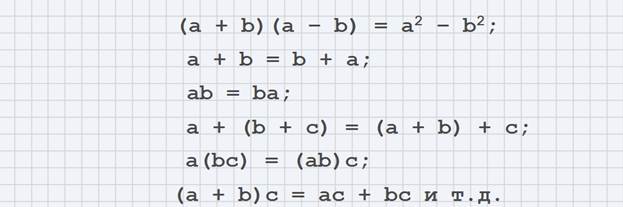
А также для действительных чисел a,b,c выполняются привычные правила:
·произведение (частное) двух положительных чисел – положительное число;
·произведение (частное) двух отрицательных чисел – положительное число;
·произведение (частное) положительного и отрицательного чисел – отрицательное число.
Действительные числа можно сравнивать друг с другом, используя следующее определение: действительное число a больше (меньше) действительного числа b, если их разность a – b – положительное (отрицательное) число.
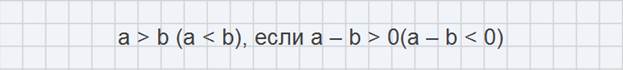
Из этого определения следует, что всякое положительное число a больше 0 (т.к. a – 0 = a является положительным числом), а любое отрицательное число b меньше 0 (т.к. разность b – 0 = b – отрицательное число).
Итак, для любых действительных a,b верно:

Все эти неравенства выполняются и для нестрогих неравенств: меньше или равно, больше или равно (![]() ). Правда в этом случае термин «положительное число» следует заменять на «неотрицательное число», т.е. положительное или 0, а термин «отрицательное число» – на «неположительное число», т.е. отрицательное или 0.
). Правда в этом случае термин «положительное число» следует заменять на «неотрицательное число», т.е. положительное или 0, а термин «отрицательное число» – на «неположительное число», т.е. отрицательное или 0.
Кроме этого, для любого числа а верно неравенство a2≥ 0; для любых чисел а и bверно неравенство (a – b)2 ≥ 0.
Для сравнения действительных чисел можно использовать не только анализ их разности, но и сделать соответствующий вывод по записи чисел в виде десятичных дробей.
Сравнивать действительные числа особенно наглядно на числовой прямой: из двух чисел больше то, которое располагается на числовой прямой правее и меньше то, которое располагается левее.
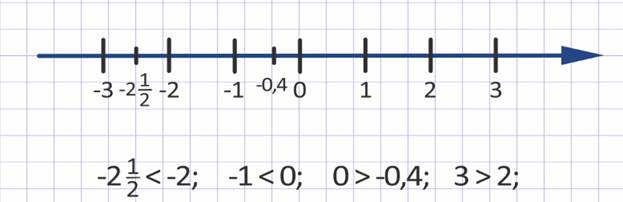
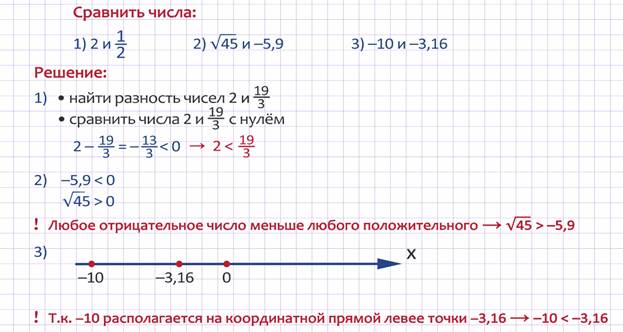
Решим несколько примеров на сравнение действительных чисел.

 Подпишись и будь
в курсе новых событий и новостей!
Подпишись и будь
в курсе новых событий и новостей!