В этом уроке сформулируем понятие «множество рациональных чисел».
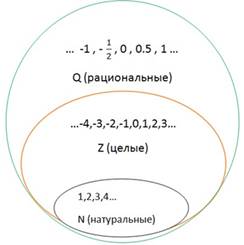
Множество рациональных чисел обозначается заглавной английской буквой Q.
Это множество включает в себя множество целых чисел (обозначается Z) и натуральных чисел (обозначается N).
Известно, что натуральные числа – это числа, которые мы используем при счете, т.е. 1,2,3,…; целые числа – это все натуральные числа 1,2,3,…., а также 0 и все целые отрицательные числа: -1,-2,-3,….
Если к множеству целых чисел Z присоединить все обыкновенные дроби: 5/7, 35/8, 66/83… , то получится множество рациональных чисел Q.
∈∉⊂⊄
Данное включение можно обозначить в виде: N ⊂ Z, Z ⊂ N.
Математический символ «⊂» называют знаком включения (одного множества в другое). Элементы x множества X принято записывать x ∈ X, знак «∈» является знаком принадлежности.
А записи «А ⊄ В» и «х ∉ Х» означают соответственно, что множество А не является частью (подмножеством) множества В, и элемент х не принадлежит множеству Х.

Рассмотрим несколько примеров использования данных математических символов для сокращения записи верных математических утверждений или, по-другому, истинных высказываний.
Пример 1:

Для всех рациональных чисел можно использовать один и тот же способ записи.
Обсудим это.
Возьмем целое число 3, его можно записать в виде бесконечной десятичной дроби 3,0000…., а также можно представить в виде бесконечной десятичной периодической дроби 3,(0):
![]()
Аналогично можно записать и десятичную дробь, например, 5,466:
![]()
А обыкновенную дробь можно представить в виде:
![]()
где повторяющуюся группу цифр после запятой называют периодом.
Таким образом, любое рациональное число можно записать в виде конечной десятичной дроби или в виде бесконечной десятичной периодической дроби.
Верно и обратное:
любую бесконечную десятичную периодическую дробь можно представить в виде обыкновенной дроби.
А значит, любая бесконечная десятичная периодическая дробь есть рациональное число.

Решение:
а) Для решения воспользуемся методом «деления углом»:
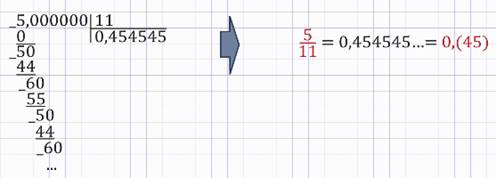
Ответ: 0,(45)
б) Для решения этого примера положим x=1,3(47)=1,3474747....
Сначала умножим x на 10, чтобы в полученном произведении период начинался сразу после запятой: 10х=13,474747....
Теперь число 10x умножим на 100, тогда запятая сместится ровно на один период вправо: 1000x=1347,474747....

Вычитаем:

Находим:
![]()
Аналогично поступаем в следующем примере
в) Пусть ![]()
Тогда
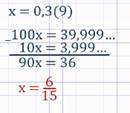
Обратите внимание, что
![]()
Таким образом, дробное число имеет две записи в виде бесконечной десятичной периодической дроби:
![]()
В последнем примере получили ![]()
Аналогично можно показать, что 0,1(9)=0,2(0) или, например, 2,46(9)=2,47(0).
Поэтому обычно десятичные дроби с периодом 9 не рассматривают, заменяют их соответствующими дробями с периодом 0.
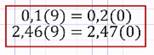
 Подпишись и будь
в курсе новых событий и новостей!
Подпишись и будь
в курсе новых событий и новостей!