Давайте вспомним свойства квадратных корней: если a, b – неотрицательные числа a, b ≥ 0, то справедливы следующие равенства:

Используя эти формулы, можно выполнять различные преобразования выражений, содержащих операцию извлечения квадратного корня, но с условием, что переменные этих выражений принимают только неотрицательные значения. Сделав такое предположение, рассмотрим несколько примеров.

Пример 1: Упросить выражение:

Поскольку в выражении присутствует дробь, для его преобразования воспользуемся вторым свойством:

Далее в числителе и знаменателе дроби используем первое свойство операции извлечения квадратного корня:

Для преобразования знаменателя использовали третье свойство:

В результате первоначальное выражение принимает вид:

Пример 2: Вынести множитель из-под знака квадратного корня:

При решении примера под буквой А воспользуемся первым и третьим свойствами квадратного корня:

Аналогично преобразуем выражение, представленное в задании под буквой Б:

Пример 3: Внести множитель под знак квадратного корня для

Чтобы внести множитель под знак корня, используем третье свойство справа налево:

Решим несколько задач по преобразованию выражений, содержащих операцию извлечения квадратного корня, пользуясь формулами сокращенного умножения. Прежде вспомним и выпишем их:

(a + b)2 = a2 + 2ab + b2

(a – b)2 = a2 – 2ab + b2

a2 – b2 = (a + b)(a – b)

a3 – b3 = (a–b)(a2 + ab + b2)

a3 + a3 = (a + b)(a2 – ab + b2)

Пример 4: Упросить выражение:

Для решения представим число три как квадратный корень из трех в квадрате:

а в знаменателе воспользуемся формулой разности квадратов, тогда получим:

Пример 5: Упростить выражение:

Решение:

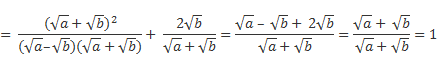
Для решения, во-первых, рассмотрим выражение:

Если предположить, что

то

используя формулу суммы кубов

Получаем

Сделаем соответствующую замену.

Во-вторых, от операции деления на (a – b) перейдем к операции умножения на обратную дробь:

В-третьих, первую дробь в скобке сократим на выражение:

а затем произведем операцию умножения.

Далее следует сложить 2 дроби с разными знаменателями. Для этого рассмотрим выражение в знаменателе первой дроби a – b

Предположим:

используя формулу разности квадратов, получаем:

Выражение в числителе первой дроби по формуле квадрата разности можно записать:

Сделаем соответствующие замены. В числителе и знаменателе первой дроби есть общий множитель, поэтому после сокращения в заключение остается только сложить дроби с одинаковыми знаменателями.

Если знаменатель алгебраической дроби содержит знак квадратного корня, то говорят, что в знаменателе содержится иррациональность. Преобразование выражения к такому виду, чтобы в знаменателе дроби не оказалось знаков квадратных корней, называют освобождением от иррациональности в знаменателе.