Не все числа, с которыми приходится встречаться в реальной жизни, являются рациональными.

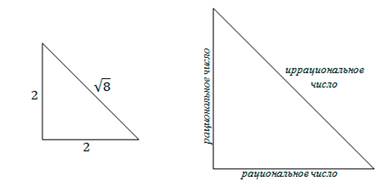
Так, не является рациональным числом длина гипотенузы с прямоугольного треугольника с катетами a= 2 см и b =2 см.

По теореме Пифагора длина гипотенузы равна:

где m – целое число, n– натуральное число.

В математике принято называть его иррациональным числом.

Примерами иррациональных чисел являются:

Если длину любой окружности разделить на ее диаметр, то в частном получится иррациональное число (число Пи ) π = 3,14159...

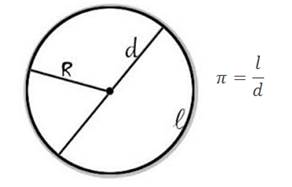
Любое иррациональное число можно записать в виде бесконечной непериодической дроби.

если точнее, то между числами 2,8 и 2,9, а еще точнее 2,82 и 2,83, продолжим уточнение, вычислим

– это бесконечная десятичная непериодическая дробь.

Итак, иррациональным числом называют бесконечную десятичную непериодическую дробь. 

Если натуральное число n не является точным квадратом, т.е.

, k – натуральное число

Мы выяснили, что помимо рациональных чисел существуют также иррациональные числа, т. е. такие, которые не являются рациональными

где m – целое число, n- натуральное число.