В этом уроке решим квадратное уравнение выделением квадрата двучлена, выведем формулы для нахождения корней полного квадратного уравнения и научимся решать квадратные уравнения по формуле.

Квадратным уравнением называют уравнение вида ax2 + bx + c = 0, где a, b, c –коэффициенты, х – переменная, причём a ≠ 0.

Левая часть квадратного уравнения ax2 + bx + c – это многочлен второй степени. Его называют квадратным трехчленом.

Полное квадратное уравнение, т.е. уравнение, в котором присутствуют все три слагаемых ax2, bx и c, можно решить выделением квадрата двучлена.

Для этого надо знать формулы сокращенного умножения: квадрат суммы и квадрат разности.

Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражения плюс квадрат второго выражения.

( a + b)2 = a2 + 2ab + b2

Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражения плюс квадрат второго выражения.

(a – b)2 = a2 – 2ab + b2

Рассмотрим примеры решения полных квадратных уравнений выделением квадрата двучлена. Сначала рассмотрим уравнение, в котором старший коэффициент a равен единице, то есть уравнение является приведенным.

Решим приведенное квадратное уравнение x2 + 6x + 8 = 0.

В квадратном трёхчлене x2 + 6x + 8 необходимо выделить квадрат двучлена. Воспользуемся формулой квадрат суммы.

Представим второй член 6x в виде произведения 2∙х∙3. Тогда для выделения квадрата двучлена к левой части уравнения необходимо прибавить и отнять число 32 = 9. Получаем (x2 + 6x + 9) – 9 + 8 = 0 или (х + 3)2 – 1 = 0.

Перенесем –1 слева направо, изменив знак.

Получим (х + 3)2 = 1.

Отсюда х + 3 = 1 и х + 3 = –1.

Значит, х1 = –2; х2 = –4

Теперь рассмотрим решение неприведенного квадратного уравнения выделением квадрата двучлена.

Решим уравнение 3х2 – 2х – 1 = 0.

Любое квадратное уравнение можно сделать приведенным.

Для этого надо обе части уравнения разделить на старший коэффициент a.

В нашем примере a = 3.

Разделим обе части уравнения на 3, получим

Это приведенное квадратное уравнение, которое решаем аналогичным предыдущему примеру способом.

Чтобы выделить квадрат двучлена в квадратном трехчлене

воспользуемся формулой квадрат разности.

Второе слагаемое

представим в виде произведения

К левой части уравнения прибавим и вычтем

Получаем

или

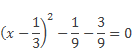
или

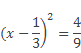
Отсюда

Значит,

Таким образом, выделением квадрата двучлена можно решить любое полное квадратное уравнение, если сделать его приведенным.

Решение квадратных уравнений выделением квадрата двучлена приводит к большим преобразованиям. Чтобы избежать этого, квадратные уравнения решают по формулам. Выведем эти формулы. Для этого к квадратному уравнению в общем виде применим метод выделения квадрата двучлена.

Решим уравнение ax2 + bx + c = 0.

Разделим обе части уравнения на a и получим равносильное приведенное квадратное уравнение

К левой части уравнения

прибавим и вычтем

Получим

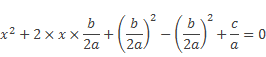
или

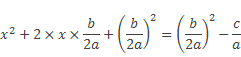
или

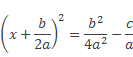
или

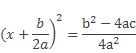
Теперь число корней уравнения ax2 + bx + c= 0 зависит от дроби

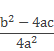
В частности, от её знака.

Знаменатель 4а2 – положительное число, поэтому знак дроби определяется числителем b2 – 4ac. Это выражение называют дискриминантом квадратного уравнения.

И обозначают буквой D.

При решении квадратного уравнения, в первую очередь, находят дискриминант D по формуле D = b2 – 4ac.

Так как от него зависит число корней уравнения.

Если D>0, то

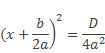
Отсюда

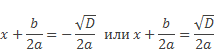
После преобразований получим

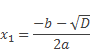
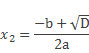
Т.е. уравнение имеет два корня.

Например, решим уравнение 3х2 – 7х + 4 = 0.

Выпишем коэффициенты a = 3, b= –7, с = 4.

Найдем дискриминант D по формуле D = b2 – 4ac.

D= (–7)2 – 4∙3∙4 = 1, D > 0, значит, уравнение имеет два корня

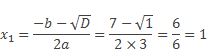
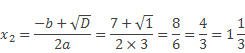
Если D=0, то

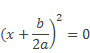
Отсюда

Значит, уравнение имеет один корень.

Например, решим уравнение 4х2 – 12х + 9 = 0.

Выпишем коэффициенты a = 4, b= –12, с = 9.

Найдем дискриминант D по формуле D = b2 – 4ac.

D= (–12)2 – 4∙9∙4 = 144 – 144 = 0.

D = 0, значит, уравнение имеет один корень.

Если D < 0, то уравнение корней не имеет.

Например, решим уравнение

2х2 + 7х + 8 = 0.

Выпишем коэффициенты a = 2, b= 7, с = 8.

Найдем дискриминант

D = b2 – 4ac = 72 – 4∙2∙8 = 49 – 64 = –15.

Так как дискриминант меньше нуля, уравнение корней не имеет.

По этим формулам можно решать как полные, так и неполные квадратные уравнения.

Важно запомнить:

При решении квадратного уравнения ax2 + bx + c = 0 по формулам поступают следующим образом:

1.находят дискриминант D по формуле D = b2 – 4ac. Значение дискриминанта зависит от коэффициентов a, b, с;

2.сравнивают дискриминант с нулём;

3.если дискриминант больше нуля, то уравнение ax2 + bx + c = 0 имеет два корня

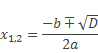
4.если дискриминант равен нулю, то уравнение имеет один корень

5.если дискриминант меньше нуля, корней нет.