В этом уроке мы познакомимся с задачами на встречное движение.
При решении любой задачи на движение мы сталкиваемся с такими понятиями, как «скорость», «время» и «расстояние».
Скорость – это расстояние, которое преодолевает объект за единицу времени. Измеряется скорость в км/ч, м/сек и т.д. Обозначается латинской буквой ʋ.
Время – это время, за которое объект преодолевает определенное расстояние. Измеряется время в секундах, минутах, часах и т.д. Обозначается латинской буквой t.
Расстояние – это путь, который преодолевает объект за определенное время. Измеряется расстояние в километрах, метрах, дециметрах и т.д. Обозначается латинской буквой S.
В задачах на движение эти понятия взаимосвязаны. Так, чтобы найти скорость, необходимо расстояние разделить на время: ʋ = S : t. Чтобы найти время, надо расстояние разделить на скорость: t = S : ʋ. А чтобы найти расстояние, скорость умножают на время: S = ʋ · t.
Говоря о задачах на встречное движение, используют понятие «скорость сближения». Скорость сближения – это расстояние, на которое сближаются объекты за единицу времени. Обозначается ʋсбл..
Чтобы найти скорость сближения при встречном движении, зная скорости объектов, надо найти сумму этих скоростей: ʋсбл. = ʋ1 + ʋ2. Чтобы найти скорость сближения, зная время и расстояние, необходимо расстояние разделить на время: ʋсбл. = S : t.
Рассмотрим взаимосвязь понятий «скорость», «время» и «расстояние» при решении задач на встречное движение.
ЗАДАЧА 1. От двух станций, расстояние между которыми 564 км, одновременно навстречу друг другу вышли два поезда. Скорость одного из них - 63 км/час. Какова скорость второго, если поезда встретились через 4 часа?
Изобразим движение поездов на схеме:
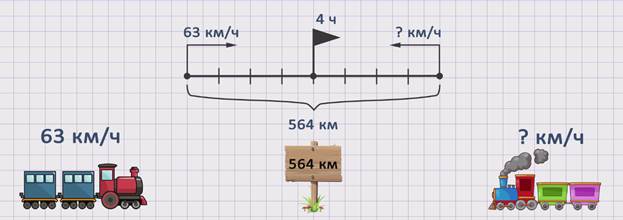
скорость первого поезда обозначим буквой ʋ1 = 63 км/ч. Скорость второго поезда обозначим буквой ʋ2 = ? км/ч. Время в пути обозначим буквой t = 4 ч. Расстояние, которое прошли оба поезда, - буквой S = 564 км.

Поскольку, чтобы найти неизвестную скорость, необходимо знать время, а оно известно и равно 4 часам, и расстояние, прошедшее вторым поездом до встречи, которое не указано в условиях задачи, то необходимо найти это расстояние.. Из условия задачи нам известно все расстояние S = 564 км, скорость первого поезда ʋ1 = 63 км/ч и время t = 4 ч. Зная расстояние, которое прошел до встречи первый поезд, мы сможем узнать и расстояние, которое прошел второй поезд. S1 = ʋ1 · t = 63 · 4 = 252 км. Значит, S2 = S – S1 = 564 – 252 = 312 км. Найдя расстояние, которое прошел до встречи второй поезд, можем найти и скорость второго поезда. ʋ2 = S2 : t = 312 : 4 = 78 км/ч. Получили, что скорость второго поезда равна 78 км/ч.

Рассмотрим второй вариант.
Поскольку, чтобы найти неизвестную скорость, необходимо знать скорость первого поезда, из условий задачи она известна ʋ1 = 63 км/ч, и скорость сближения, которая не оговаривается условиями задачи, то надо найти скорость сближения, используя данные задачи, а именно расстояние S = 564 км и время встречи t = 4 часа. Чтобы найти скорость сближения поездов, можно расстояние разделить на время. ʋсбл. = S : t = 564 : 4 = 141 км/ч. Теперь, зная скорость сближения, можем найти скорость второго поезда. ʋ2 = ʋсбл. - ʋ1 = 141 – 63 = 78 км/ч. Получили, что скорость второго поезда равна 78 км/ч.
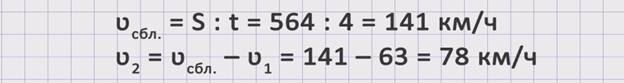
ЗАДАЧА 2. Расстояние между двумя пристанями 90 км. От каждой из них одновременно навстречу друг другу вышли два теплохода. Сколько часов им понадобится, чтобы встретиться, если скорость первого составляет 20 км/час, а второго – 25 км/час?
Изобразим движение теплоходов на схеме.
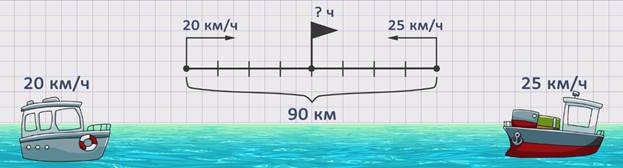
Скорость первого теплохода обозначим буквой ʋ1 = 20 км/ч. Скорость второго теплохода обозначим буквой ʋ2 = 25 км/ч. Расстояние между пристанями обозначим буквой S = 90 км. Время – буквой t = ? часов.
Чтобы ответить на поставленный вопрос задачи, необходимо знать расстояние и скорость сближения, так как t = S : ʋсбл.. Поскольку расстояние нам известно из условия задачи, надо найти скорость сближения. ʋсбл. = ʋ1 + ʋ2 = 20 + 25 = 45 км/ч. Теперь, зная скорость сближения, можем найти неизвестное время. t = S : ʋсбл = 90 : 45 = 2 ч. Получаем, что теплоходам понадобится 2 часа, чтобы встретиться.
ЗАДАЧА 3. Из поселка и города навстречу друг другу одновременно выехали два автобуса. Один автобус до встречи проехал 100 км со скоростью 25 км/час. Сколько километров до встречи проехал второй автобус, если его скорость - 50 км/час?
Покажем движение автобусов на схеме.
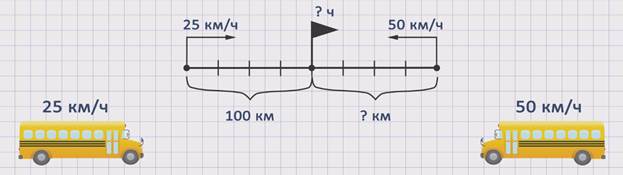
Скорость первого автобуса обозначим буквой ʋ1 = 25 км /ч. Скорость второго автобуса обозначим буквой ʋ2 = 50 км/ч. Расстояние, которое до места встречи проехал первый автобус, обозначим буквой S1 = 100 км. Расстояние, которое проехал до встречи второй автобус – буквой S2 = ? км, а время – буквой t.
Чтобы ответить на вопрос задачи, необходимо знать скорость второго автобуса и время, которое он был в пути до встречи, так как S2 = ʋ2 · t. Поскольку скорость второго автобуса известна из условия задачи, надо найти время. Если мы найдем время, которое был в пути первый автобус, то мы найдем и время, которое был в пути второй автобус, так как они выехали одновременно, а это значит, что до момента встречи автобусы были в пути одинаковое количество времени. Чтобы найти время, можно расстояние, которое проехал первый автобус, разделить на его скорость. t = S1 : ʋ1 = 100 : 25 = 4 часа. Теперь, зная время, можем найти расстояние, которое второй автобус проехал до момента встречи. S2 = ʋ2 · t = 50 · 4 = 200 км. Получили, что второй автобус проехал до встречи 200 км.
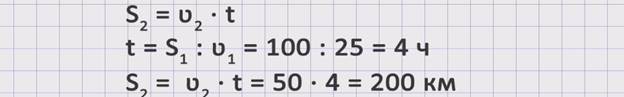
При решение задач на встречное движение следует помнить, что в задачах такого типа выполняются следующие условия:
1.Объекты начинают свое движение одновременно навстречу друг другу, т.е. находятся в пути до встречи одинаковое количество времени; время обозначается латинской буквой t = S : ʋсбл;
2.Расстояние S – это сумма расстояний двух объектов до встречи; S = S1 + S2 или S = ʋсбл· t;
3.Объекты сближаются с определенной скоростью – скоростью сближения, обозначающейся латинской буквой ʋсбл. = S : t или ʋсбл = ʋ1 + ʋ2, соответственно ʋ1 = S1 : t и ʋ2 = S2 : t.
 Подпишись и будь
в курсе новых событий и новостей!
Подпишись и будь
в курсе новых событий и новостей!