С формулами одновременного движения мы сталкиваемся при решении задач на одновременное движение. Умение решать ту или иную задачу на движение зависит от некоторых факторов. Прежде всего, необходимо различать основные типы задач.

Задачи на одновременное движение условно делятся на 4 типа: задачи на встречное движение, задачи на движение в противоположных направлениях, задачи на движение вдогонку и задачи на движение с отставанием.

Основными компонентами этих типов задач являются:

пройденный путь – S, скорость - ʋ, время – t.

Зависимость между ними выражается формулами:

S = ʋ · t, ʋ = S : t, t = S : ʋ.

Помимо названных основных компонентов при решении задач на движение мы можем столкнуться с такими компонентами, как: скорость первого объекта - ʋ1, скорость второго объекта – ʋ2, скорость сближения – ʋсбл., скорость удаления – ʋуд., время встречи – tвстр., первоначальное расстояние – S0 и т.д.

При решении задач данного типа применяются следующие компоненты: скорость первого объекта - ʋ1; скорость второго объекта - ʋ2; скорость сближения – ʋсбл.; время до встречи – tвстр.; путь (расстояние), пройденный первым объектом – S1; путь (расстояние), пройденный вторым объектом - S2; весь путь, пройденный обоими объектами – S.

Схема к задачам такого типа выглядит следующим образом:

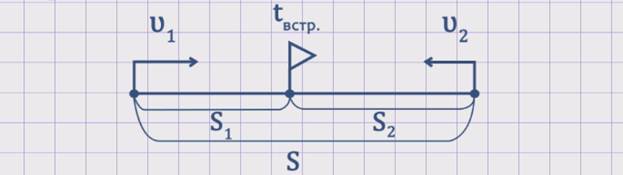
Зависимость между компонентами задач на встречное движение выражается следующими формулами: 

1.первоначальное расстояние между объектами можно вычислить по следующим формулам: S = ʋсбл. · tвстр. или S = S1 + S2;

2.скорость сближения находится по формулам: ʋсбл. = S : tвстр. или ʋсбл. = ʋ1 + ʋ2;

3.время встречи вычисляется следующим образом:

tвстр. = S : ʋсбл., tвстр. = S1 : ʋ1 или tвстр. = S2 : ʋ2.

Рассмотрим применение данных формул на примере следующей задачи.

Два теплохода плывут навстречу друг другу. Скорости теплоходов 35 км/ч и 28 км/ч. Через какое время они встретятся, если расстояние между ними 315 км?

ʋ1 = 35 км/ч, ʋ2 = 28 км/ч, S = 315 км, tвстр. = ? ч.

Чтобы найти время встречи, необходимо знать первоначальное расстояние и скорость сближения, так как tвстр. = S : ʋсбл. Поскольку расстояние известно по условию задачи, найдем скорость сближения. ʋсбл. = ʋ1 + ʋ2 = 35 + 28 = 63 км/ч. Теперь можем найти и искомое время встречи. tвстр. = S : ʋсбл = 315 : 63 = 5 ч. Получили, что теплоходы встретятся через 5 часов.

При решении задач данного типа применяются следующие компоненты: скорость первого объекта – ʋ1; скорость второго объекта - ʋ2; скорость сближения – ʋсбл.; время до встречи – tвстр.; путь (расстояние), пройденный первым объектом – S1; путь (расстояние), пройденный вторым объектом – S2; первоначальное расстояние между объектами – S.

Схема к задачам такого типа выглядит следующим образом:

Зависимость между компонентами задач на движение вдогонку выражается следующими формулами:

1.Первоначальное расстояние между объектами можно вычислить по следующим формулам:

S = ʋсбл. · tвстр.илиS = S1 - S2;

2.скорость сближения находится по формулам: ʋсбл. = S : tвстр. или ʋсбл. = ʋ1 - ʋ2;

3.Время встречи вычисляется следующим образом:

tвстр. = S : ʋсбл., tвстр. = S1 : ʋ1 или tвстр. = S2 : ʋ2.

Рассмотрим применение данных формул на примере следующей задачи.

Тигр погнался за оленем и догнал его через 7 минут. Каково первоначальное расстояние между ними, если скорость тигра равна 700 м/мин, а скорость оленя - 620 м/мин?

ʋ1 = 700 м/мин, ʋ2 = 620 м/мин, S = ? м, tвстр. = 7 мин.

Чтобы найти первоначальное расстояние между тигром и оленем, необходимо знать время встречи и скорость сближения, так как S =tвстр. · ʋсбл. Поскольку время встречи известно по условию задачи, найдем скорость сближения. ʋсбл. = ʋ1 - ʋ2 = 700 – 620 = 80 м/мин. Теперь можем найти и искомое первоначальное расстояние. S =tвстр. · ʋсбл = 7 · 80 = 560 м. Получили, что первоначальное расстояние между тигром и оленем составляло 560 метров.

При решении задач данного типа применяются следующие компоненты: скорость первого объекта – ʋ1; скорость второго объекта – ʋ2; скорость удаления – ʋуд.; время в пути – t.; путь (расстояние), пройденный первым объектом – S1; путь (расстояние), пройденный вторым объектом – S2; первоначальное расстояние между объектами – S0; расстояние, которое будет между объектами через определенное время – S.

Схема к задачам такого типа выглядит следующим образом:

Зависимость между компонентами задач на движение в противоположных направлениях выражается следующими формулами:

1.Конечное расстояние между объектами можно вычислить по следующим формулам:

S = S0 + ʋуд.· tили S = S1 + S2 + S0; а первоначальное расстояние – по формуле: S0 = S - ʋуд. · t.

2.Скорость удаления находится по формулам:

ʋуд. = (S1 + S2) : t илиʋуд. = ʋ1 + ʋ2;

3.Время в пути вычисляется следующим образом:

t = (S1 + S2) : ʋуд., t = S1 : ʋ1или t = S2 : ʋ2.

Рассмотрим применение данных формул на примере следующей задачи.

Два автомобиля выехали из автопарков одновременно в противоположных направлениях. Скорость одного – 70 км/час, другого – 50 км/час. Какое расстояние будет между ними через 4 часа, если расстояние между автопарками составляет 45 км?

ʋ1 = 70 км/ч, ʋ2 = 50 км/ч, S0 = 45 км, S = ? км, t = 4 ч.

Чтобы найти расстояние между автомобилями в конце пути, необходимо знать время в пути, первоначальное расстояние и скорость удаления, так как S = ʋуд. · t+ S0Поскольку время и первоначальное расстояние известны по условию задачи, найдем скорость удаления. ʋуд. = ʋ1 + ʋ2 = 70 + 50 = 120 км/ч. Теперь можем найти и искомое расстояние. S = ʋуд. · t+ S0 = 120 · 4 + 45 = 525 км. Получили, что через 4 часа между автомобилями будет расстояние в 525 км

При решении задач данного типа применяются следующие компоненты: скорость первого объекта – ʋ1; скорость второго объекта – ʋ2; скорость удаления – ʋуд.; время в пути – t.; первоначальное расстояние между объектами – S0; расстояние, которое станет между объектами через определенное количество времени – S.

Схема к задачам такого типа выглядит следующим образом:

Зависимость между компонентами задач на движение с отставанием выражается следующими формулами:

1.Первоначальное расстояние между объектами можно вычислить по следующей формуле: S0 = S - ʋуд.· t; а расстояние, которое станет между объектами через определенное время, - по формуле: S = S0 + ʋуд. · t;

2.Скорость удаления находится по формулам: ʋуд.= (S – S0) : t или ʋуд. = ʋ1 - ʋ2;

3.Время вычисляется следующим образом: t = (S – S0) : ʋуд.

Рассмотрим применение данных формул на примере следующей задачи:

Из двух городов в одном направлении выехали две машины. Скорость первой – 80 км/ч, скорость второй – 60 км/ч. Через сколько часов между машинами будет 700 км, если расстояние между городами 560 км?

ʋ1 = 80 км/ч, ʋ2 = 60 км/ч, S = 700 км, S0 = 560 км, t = ? ч.

Чтобы найти время, необходимо знать первоначальное расстояние между объектами, расстояние в конце пути и скорость удаления, так как t = (S – S0) : ʋуд. Поскольку оба расстояния известны по условию задачи, найдем скорость удаления. ʋуд. = ʋ1 - ʋ2 = 80 – 60 = 20 км/ч. Теперь можем найти и искомое время. t = (S – S0) : ʋуд = (700 – 560) : 20 = 7ч. Получили, что через 7 часов между машинами будет 700 км.

При одновременном встречном движении и движении вдогонку расстояние между двумя движущимися объектами уменьшается (до встречи). За единицу времени оно уменьшается на ʋсбл., а за все время движения до встречи оно уменьшится на первоначальное расстояние S. Значит, в обоих случаях первоначальное расстояние равно скорости сближения, умноженной на время движения до встречи: S = ʋсбл. · tвстр.. Разница лишь в том, что при встречном движении ʋсбл. = ʋ1 + ʋ2, а при движении вдогонку ʋсбл. = ʋ1 - ʋ2.

При движении в противоположных направлениях и с отставанием расстояние между объектами увеличивается, поэтому встреча не произойдет. За единицу времени оно увеличивается на ʋуд., а за все время движения оно увеличится на значение произведения ʋуд.· t. Значит, в обоих случаях расстояние между объектами в конце пути равно сумме первоначального расстояния и произведения ʋуд.· t. S = S0 + ʋуд.· t.Разница лишь в том, что при противоположном движении ʋуд. = ʋ1 + ʋ2, а при движении с отставанием ʋуд. = ʋ1 - ʋ2.